こんにちは。Horyです。
前回の記事では弦の振動と音が関係する気中共鳴問題に取り組みました。
今回の記事ではドップラー効果について現象の意味を説明するとともに原理を解説します。
ドップラー効果は混乱する学生が多いような印象を受けます。
今回も頑張りましょう。
ドップラー効果
まず、ドップラー効果とは「音源が動いている場合や観測者が動いている場合に、耳にする音の振動数が音源から出ている本来の音よりも高かったり低かったりする現象」のことです。
ドップラー効果では基本的に波長や振動数を求める問題が非常に多く、パターンがいくつかあります。
この記事では３つのパターンに関して解説します。
- パターン①；音源が等速で動く場合、音源から見た音波の波長
- パターン②；音源が静止、観測者が等速で動く場合、観測者から見た音波の振動数
- パターン③；音源と観測者が等速で動く場合、観測者から見た音波の振動数
これらの3つに関して個別に解説していきたいと思います。
パターン①
音源が等速で動いているときに音源から見た音波の波長を求めます。
分かりやすいように図を用いて解説します。
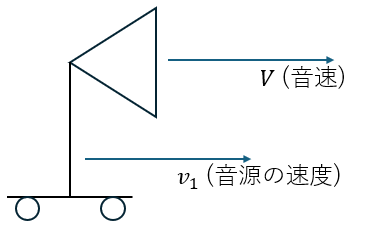
- 音源の速度；v1 (等速)
- 音速；V
- 音源から見た音波の振動数；f1
- 音源から見た音波の波長 (空気中)；λ
観測者が音源上に乗っている状態で音波を観測すると考えます。
音源が観測する音波の振動数と波長を考えます。
- 振動数；音源と共に移動しているので変化しない
- 波長；伸び縮みが起きる
振動数が変わらない理由ですが、この記事で解説した境界条件を思い出してください。
音源から出た音は異なる媒質である空気中にすり抜けて透過します。
つまり、異なる媒質の境界では境界条件が成立し、境界では任意の時間において位相が完全一致するので・・・
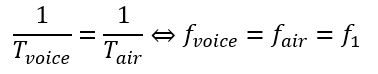
次に波長がどのように変化するかを求めます。
音源を観測者として見たとき、空気中を進行する音の速度がどうなるかを求めます。
相対速度に関してはこちらの記事で解説した通りです。
以上がパターン①の解説になります。
パターン②
音源が静止、観測者が等速で動く場合、観測者から見た音波の振動数を求めます。
分かりやすいように図を用いて解説します。
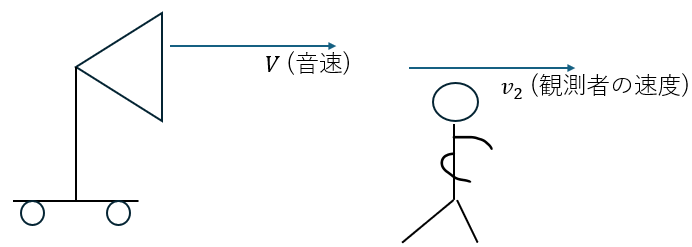
今度は観測者が動いていて音源は静止しているので波長は変化しません。
しかし、観測者が観測する音波の振動数は変化します。
- 観測者の速度；v2 (等速)
- 音速；V
- 観測者から見た音波の振動数；f2
- 観測者から見た音波の波長 (空気中)；λ (変化なし)
観測者から見た音波の振動数を求めてみます。
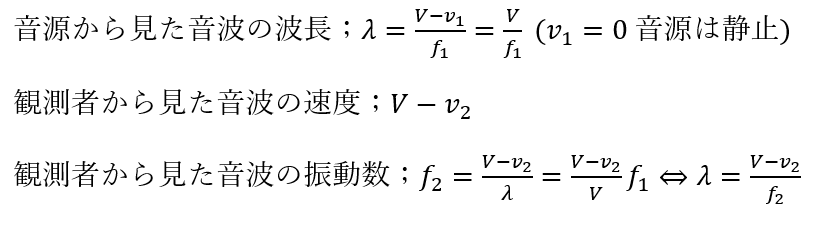
以上がパターン②の解説になります。
ちなみに、観測者が音波を観測するときも境界条件が使われます(空気から鼓膜への媒質の変化による境界条件)。
境界条件により振動数はf2のままで一定です。
パターン③
音源と観測者が等速で動く場合を考えてみます。
これはパターン①とパターン②の融合になります。
これをまとめると・・・
以上がドップラー効果になります。
