こんにちは。Horyです。
今回の問題では弦の振動と音の振動に関して気柱共鳴問題を攻略していきたいと思います。
本記事で紹介する問題も頻出する問題なので必ず理解したい問題です。
今回も頑張りましょう。
気柱共鳴問題
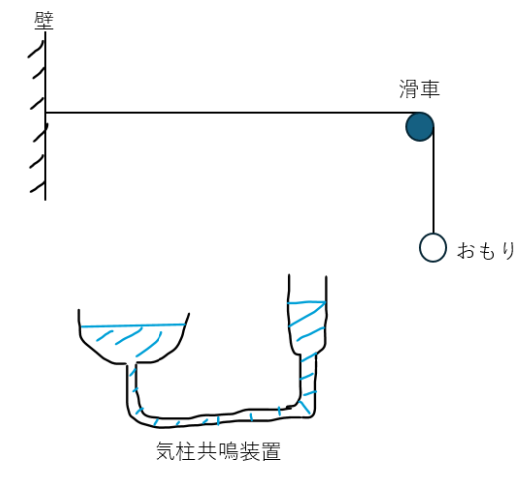
以下に示すのは本記事で紹介する気柱共鳴問題です。

この問題を例に解説します。まぁ、聞いたことのない言葉もあるので事前準備をしっかりと行いましょう。
問題を解く前の下準備
まずは、問題を解く前の下準備から始めます。
面密度という聞き慣れない言葉が出てきましたが、弦というのは糸で出来ています。この糸の単位長さ当たりの質量を面密度と言います。
弦を伝わる波の速さは弦の張力と面密度の比の平方根に等しいので、糸の張力をS[N]として面密度をρ[kg/m]とすると速さは以下のように記述できます。
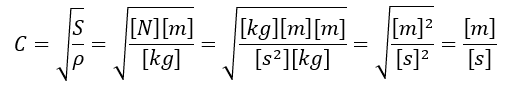
この速度は力学的条件で決定されます。
わかりやすさのために図を用いて解説します。
綿密度に関して運動方程式を立てると・・・
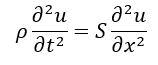
この式はどこかで見たことありますねぇ。この記事でも紹介したダランベールの解です。
そのため、右向きの進行波と左向きの進行波が発生します。
波の反射の記事でも解説しましたが、弦の振動は固定端反射です。
そのため・・・右向き、左向き進行波の合成波は定常波になります(Cを位相速度とする)。
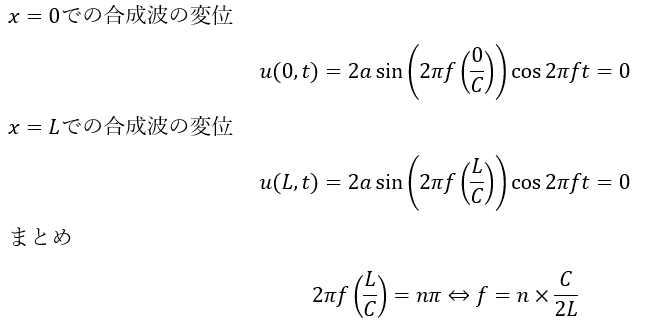
固定端での定常波は0になります(前回の記事で解説した)。
上に示す値の振動数の固有振動が生じます(固有振動とは物体の性質に基づいた振動ということです。今回であれば、おもりや弦の材質はこの問題に固有のもので、振動が問題の条件に固有のものであるという意味です)。
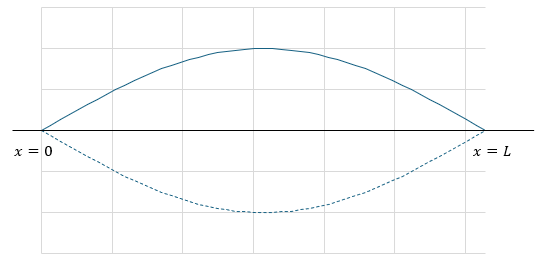
ちなみに、振動には基本振動・二倍振動・三倍振動・・・と続いていき、図で解説すると・・・
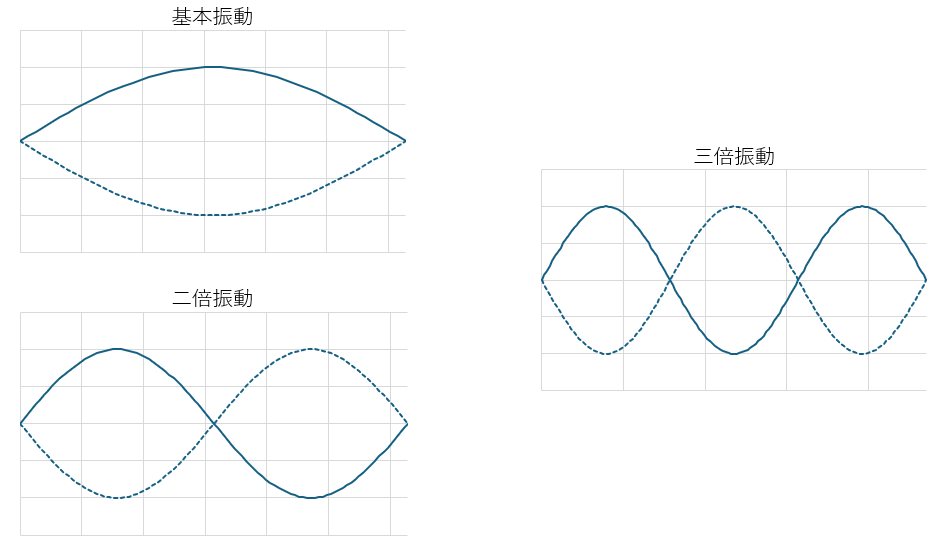
これで事前準備は完了です。問題を解いていきましょう。
(1)解答・解説
問題を解いていきます。おもりの重力と張力は釣り合っています。
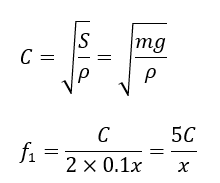
以上が解答になります。基本振動は半波長の波動が弦に現れます。また、注意してほしいのが単位で壁と滑車間の長さがmではなくcmです。
単位を軽視する人はこういうところで失点するので気を付けましょう。
(2)解答・解説
基本振動後は弦の振動と同じ振動数の音波が生じます。
音波は水面で反射します。この反射は固定端反射です。そのため、管内には定常波が生じます。
図を用いて解説します。
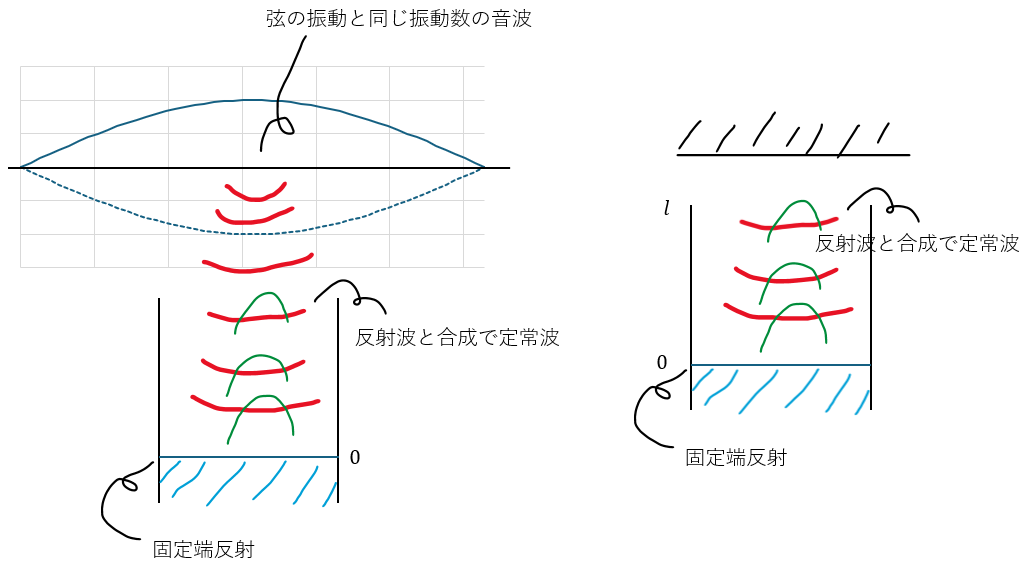
また、開口端についても解説します。開口端は外部の空気と同密度になるように反射します。
管内の位置xでの音波による空気の変位は以下のように書けます(C1は管内の音波の速さとする)。
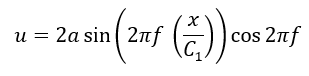
ここで、音波は縦波ということも前回の記事で解説しました、そのため、疎密があります。
空気変位と密度変化のグラフに関しては覚えておいた方がいいです。
図に例を示します。
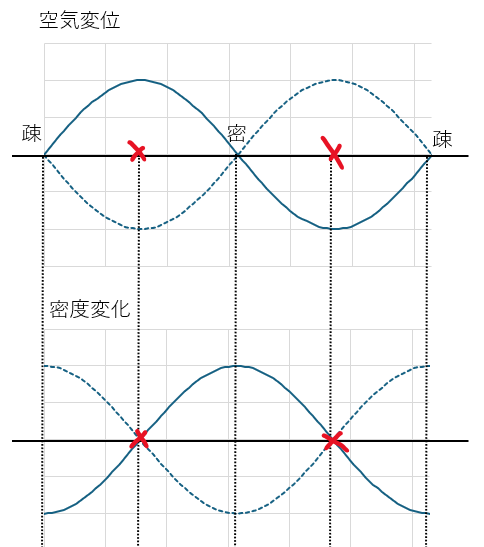
疎密の位置はこの記事でも解説した通りです。
図から分かることとして空気変位の節のところで密度変化(の絶対値)が最大になります。
開口端補正について解説します。空気変化は開口端で必ず腹になります。
気中の長さでそのまま考えるのではなく開口端部を補正する必要があります。
まぁ、図を用いて説明した方が分かりやすいので図を示します。
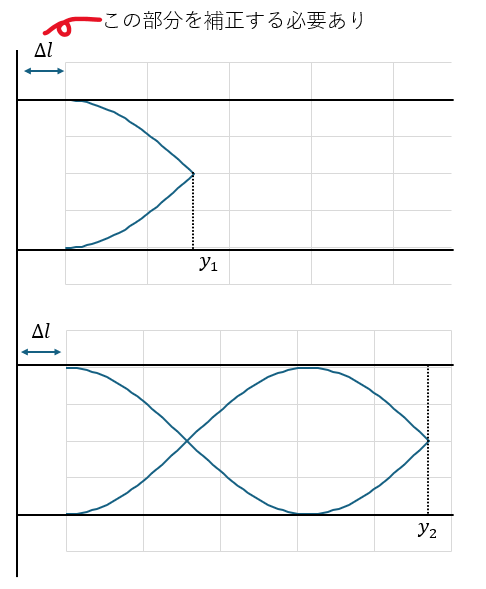

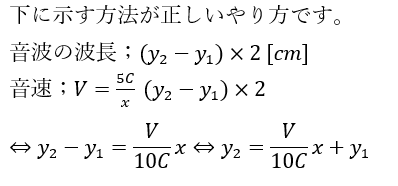
(3)解答・解説
うなりについてはこちらの記事でも解説した通りですが・・・
弦の位置を「x=0」にとってこの位置での波の合成を考えます。今は、振動数を考えるだけなので、いったん、A=Bとして和積公式を用います。
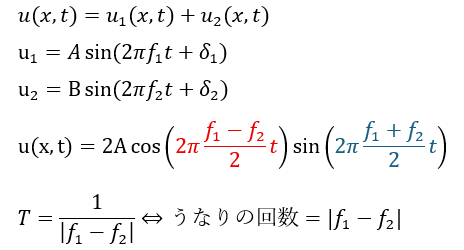
上の式の赤い部分と青い部分のどちらをうなりの回数として信じるのかについてですが(二つの波動の積になっている)・・・
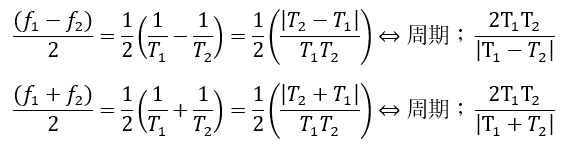
二つの波動の周期がほぼ等しい場合は赤と青の部分のどちらの周期が非常に大きいでしょうか?
赤い部分の周期が大きくなりますよね。だから、人間の耳に断続的にうなりとして聞こえるのです。
よってうなりの回数として信じるのは赤い部分です。