こんにちは。Horyです。
前回の記事では正弦波の問題について解説しました。
今回の記事では正弦波の式についてちょっと深く掘り下げようと思います。
というのも、昔、教えていた多くの学生から「正弦波の式が二つあってどちらを使えばいいか困る」という質問をよく受けたからです。
今回はこの問題に関して掘り下げようと思います。
今回も頑張りましょう。
正弦波の二つの式
正弦波の二つの式というのは以下の式のことです。
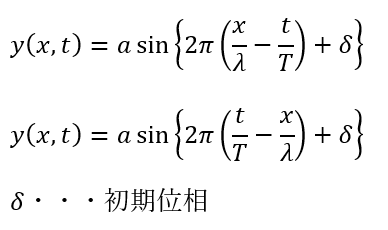
上の二つの正弦波の式の内、一番上のやつはこちらの記事で解説しました。
二つの式のどちらが正しいのか分からないという人がいますが、結論から言うと、「どちらも同じ式」です。
ただし、正弦波の変位の式をどの視点から見るかという意味で違いが出ているだけです。
以下ではその違いを解説します。
変位と位置のグラフから考える
変位と位置のグラフから正弦波の式を考えます。
「t=0」の時の正弦波のグラフを以下のように考えます。
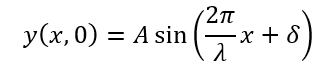
ここで、tを何とかして出していきたいので、この波動がCtだけ進んだ位置での位相を式で表します(Cは位相速度)。
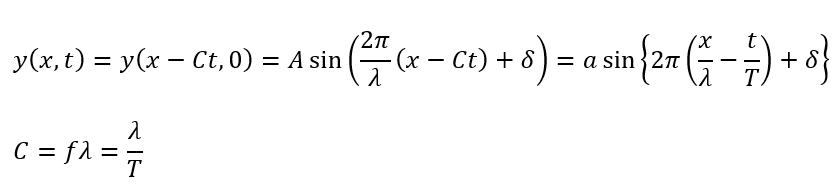
何度も言っていますが、ただの平行移動です(これは前回の記事で求めた)。
変位と時間のグラフから考える
変位と時間のグラフから正弦波の式を考えます。
「x=0」の正弦波のグラフを以下のように定義します。
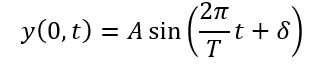
ここで、何とかしてxを出したいので、「x/C秒」だけ進んだ波の位相の式を考えます。
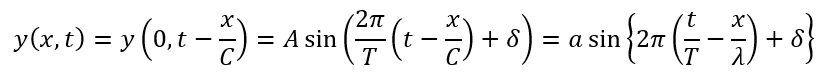
以上から求めることができました。
まとめ
これらの式の違いは「どの視点から正弦波の式を見ているのか」という違いです。
だから、問題から正弦波の式を考えるときは以下のことに注意してください。
- 変位と位置の関係式がある
- 時間がt=0の正弦波の式を作る y(x,0)
- 位置が「x=Ct」だけ進んだ位置での位相の式を求める
- y(x,t)=y(x-Ct,0)で正弦波の式を求める
- 変位と時間の関係式がある
- 位置がx=0の正弦波の式を作る y(0,t)
- 時間が「t=x/C」だけ進んだ時での位相の式を求める
- y(x,t)=y(0,t-x/C)で正弦波の式を求める



コメント