こんにちは。Horyです。
前回の記事ではマクスウェル方程式について解説しました。
今回の記事ではマクスウェル方程式を応用して電磁波の性質を解説しようと思います。
今回も頑張りましょう。
マクスウェル方程式
まずは、前回の復習でマクスウェル方程式を微分系で書き下してみます。

- ガウスの法則 (電場);空間中に電荷を持つ物体を置くと電場が発生
- ガウスの法則 (磁場);磁石は必ずNとS極でペアになる (磁力線のループ)
- マクスウェル・アンペール則;電場の変化で磁場が発生する
- ファラデーの電磁誘導の法則;磁場の発生で磁場の変化を妨げる向きに電場が発生する。
ここまでがマクスウェル方程式のおさらいになります。
電場や磁場に成立する関係式
電場や磁場に成立する関係式を簡単に紹介します。
- 空間中の電場;D_誘電率を用いる
- 磁束密度(物質中の磁場);H(磁場)_を用いる
- 電流密度(単位面積当たりの電流);σ_抵抗率を用いる
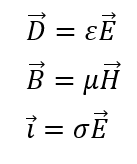
- ε・・・空間の誘電率
- μ・・・空間中の透磁率
- σ・・・電気伝導率 (電気抵抗率の逆数)
この中で、3番目に出てくる単位面積当たりの電流密度と電場の関係式は見たことがないので解説します。
電流や抵抗の関係はこちらの記事でも解説しました。

求めた式はある意味でオームの法則であるとも言えます。念のため、次元検算も行います。
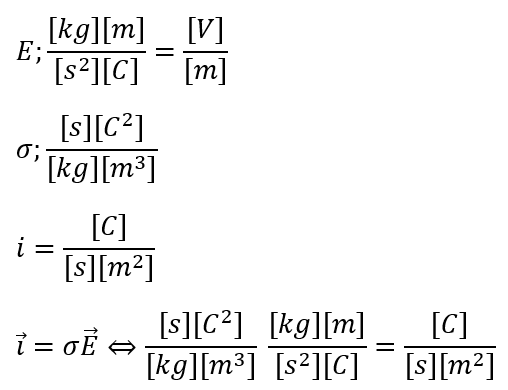
確かに、基本単位を用いて次元検算しても次元が一致するので合っていそうです。
この式を用いてマクスウェル・アンペール則を書き直すと・・・
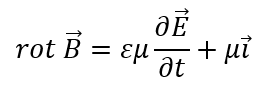
マクスウェル・アンペール則の発散を取る
マクスウェル・アンペール則の両辺にdivを取ってみましょう。
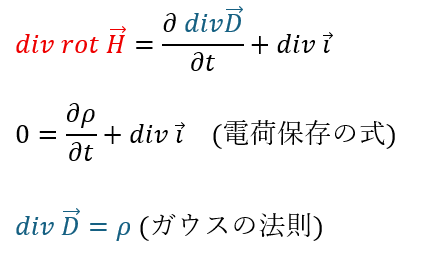
赤い部分ですが、微分演算子の通りに計算すると0になります。
証明はこの記事でやったので今回はしませんが、考えてみれば分かると思います。
- rot・・・回転を取っている
- div・・・発散を取る
- div rot・・・回転してループしてる量の発散は0になる (当たり前)
電荷保存の式の意味は「単位時間当たりに出て行く電気量は流れ出る電流の量と一致する」と言うことを表しています。
実際に積分系を書いてみると・・・
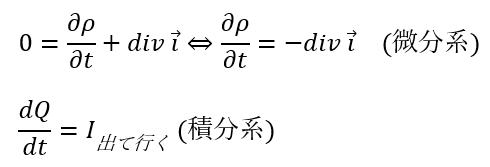
ファラデーの電磁誘導の法則を変形
磁束密度のベクトルポテンシャルを取ります。
ビオサヴァールの法則を解説する際に、ベクトルポテンシャルは用いたかもしれないですが、同じ操作をしてあげます。
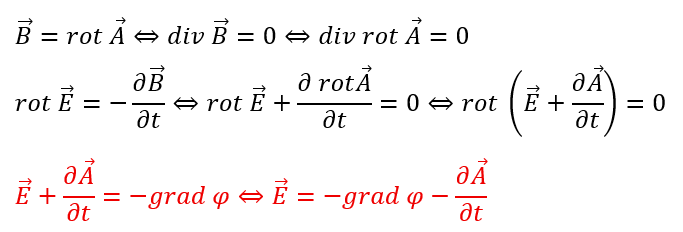
上の式の色が付いた部分は電位ポテンシャルφ(スカラー)に∇を作用させたものになります。
ガウス則とアンペール則の連立
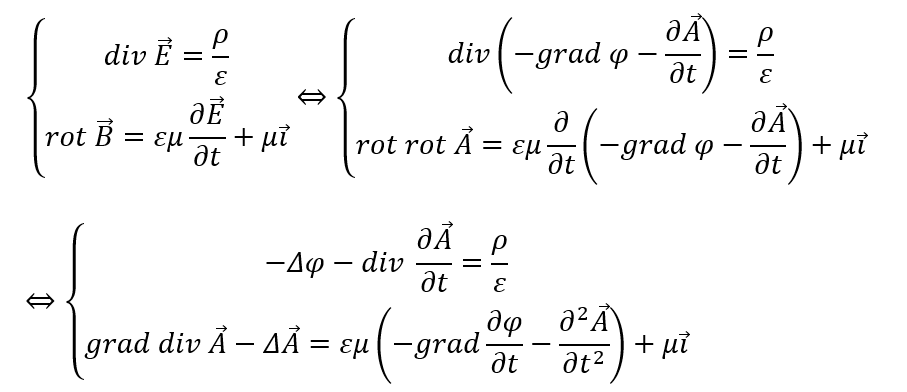
ここからどうしたモノかと思いますが、div Aをなんとかしたいので以下の式を用います。
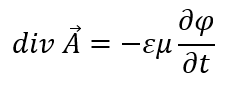
この式のことをローレンツゲージと呼びます。一旦、「ふーん」程度に思ってください。
ローレンツゲージに関しては僕のやる気があれば解説します。
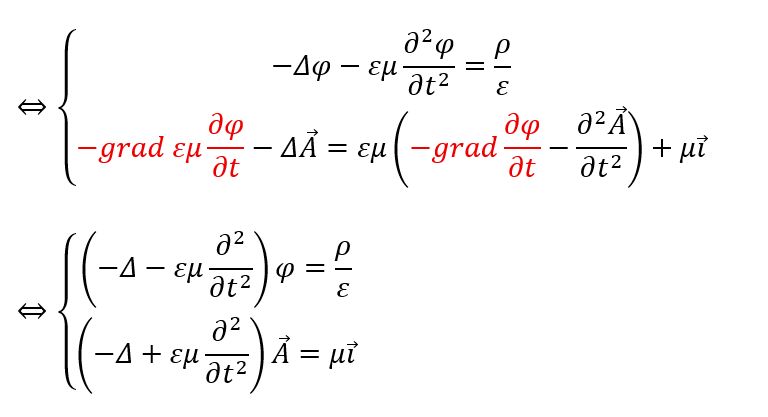
真空中での電場・磁場の波動方程式
真空中での電場の波動方程式を求めます。
真空中であると言うことは電荷も電流も存在しません。
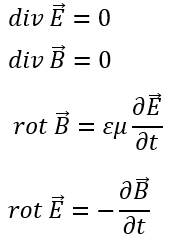
ファラデーの電磁誘導の法則の両辺にrotを取ります。
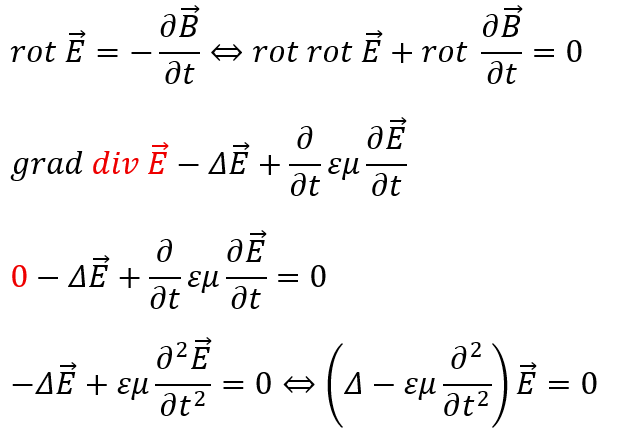
磁場に関しても同様の操作を行います。
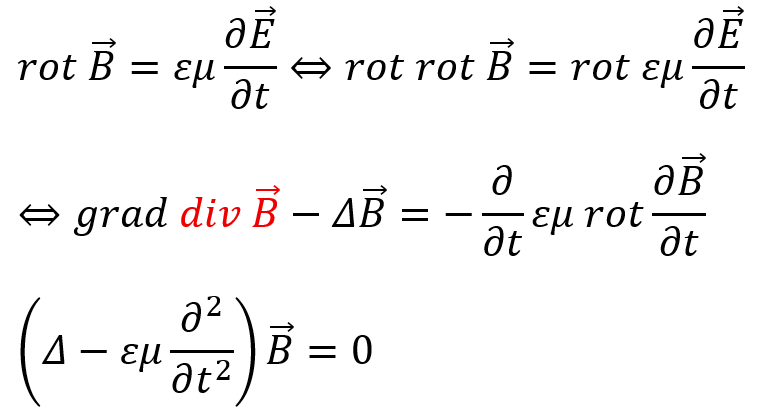
同じような式が最終的に導かれます。
波動方程式の成分表示 (簡単な表示)
波動方程式を簡単な場合で成分表示してみます。
仮に、電場と磁束密度の全ての成分がzの値のみで決定されると考えると・・・
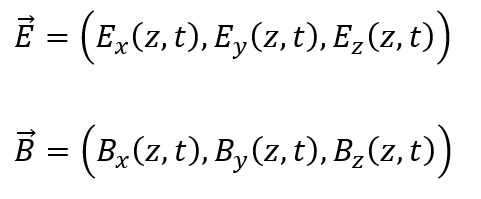
これを以下の二式に代入して考えてみます。
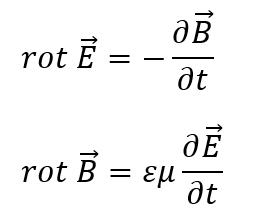
電場の回転をまずは求めてみます。
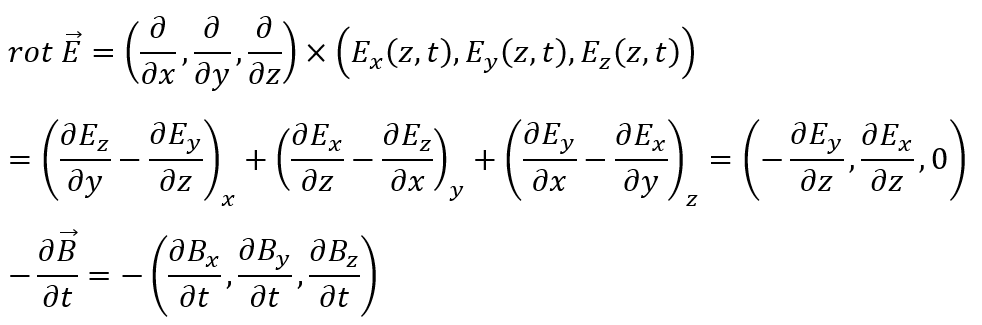
成分が一致しないといけないので・・・
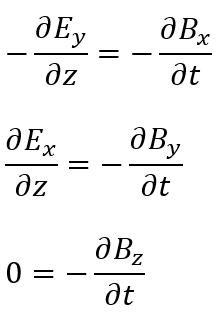
磁束密度に関しても同様のことを行うと・・・
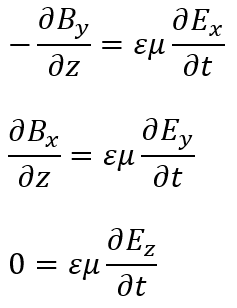
また、ガウスの法則を用いると・・・
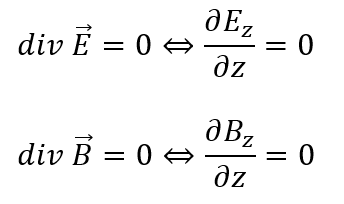
上の式ですが、電場と磁束密度のx,y,z方向も位置zの関数によって決定されるのでdivのx,y成分は当然0になります(当たり前)。
上の式で0になっている部分を利用すると・・・
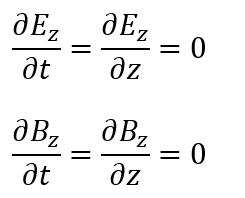
上の2つの式が意味することは、電場も磁場も時間と場所によらない定数でアルコとを意味しています。
時間にも場所にも依存しないと言うことは静電場、静磁場と言うことに他なりません。
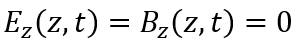
今は、電場がx方向にのみ進行すると考えると・・・
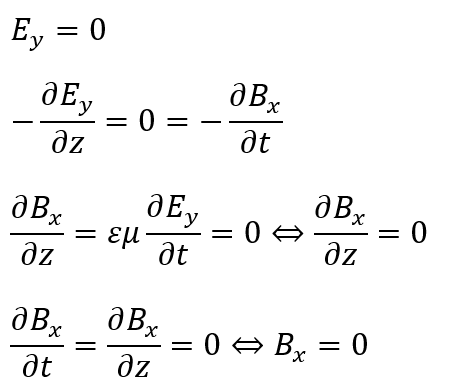
以上から磁場はy方向にのみ進行することが明らかになりました。
もう予想できると思いますが、電場と磁場は直交すると考えられます。
電波と磁波の性質 (電磁波の性質)
一般的な電波の磁波の性質を考えてみます。
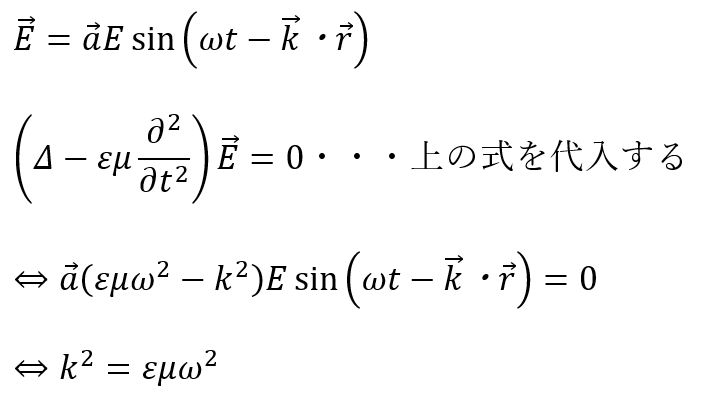
ωが周波数であることと、kが距離2π中の波の数であることを考慮すると・・・
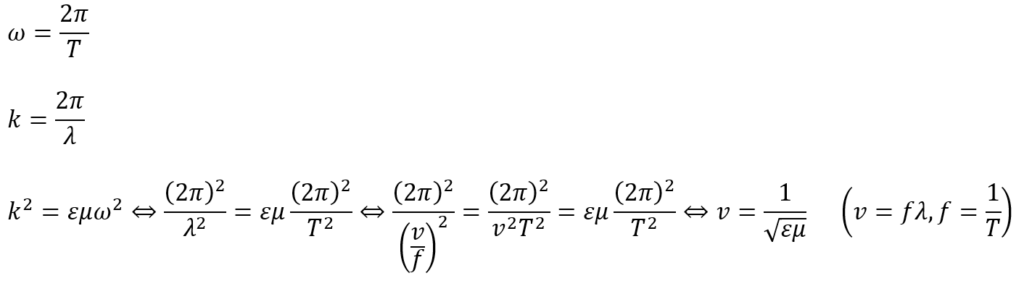
上の式から電波の速さを求めることができました。磁波も同様の速さになります。
これを真空中のクーロンの法則に代入してみます。
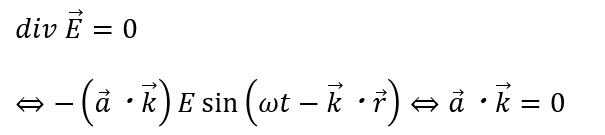
上の式の意味することは波の進行方向(ベクトルk)について電波の方向(ベクトルa)は垂直であるという点です。
以上のことから電波は横波と言うことが分かります。
一方で磁波に関しても・・・
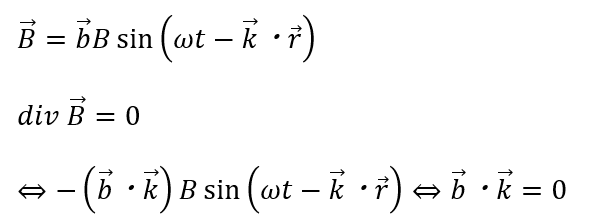
同様に波の進行方向と磁波の進行方向は垂直に交わります。
このことから磁波も横波です。
これにより波の進行方向と電波・磁波の関係性が分かりました。
最後に分かっていないのが電波と磁波の関係性です。これを求めていきます。
ファラデーの電磁誘導の法則を用いると・・・
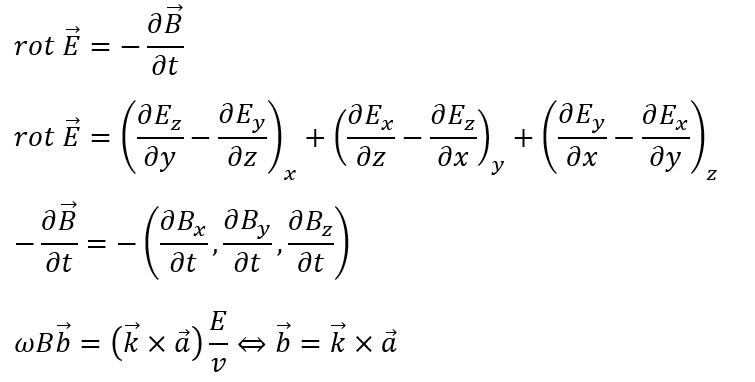
計算をだいぶ省略しましたが許してください(体力の限界を感じた)。
上の式が意味するところは磁場の進行方向が電場の進行方向と波の進行方向の外積を取った方向にあると言うことです(外積の記事で右ネジが空間的に進む方向と考えると・・・)。
このことから、電波と磁波も直交している事が分かります。
結論ですが、「電磁波の進行方向(波そのものの進行方向)と電場の方向、磁場の方向は互いに直交します。」



コメント