こんにちは。Horyです。
前回の記事では自己誘導・相互誘導について学ぶと共に、コイルについて簡単に解説しました。
今回の記事では抵抗とコイルが直列に繋がれたRL直列回路における過渡現象について考えようと思います。
過渡現象と言えば、抵抗とコンデンサが直列に接続されたRC直列回路でもやったと思います。
過渡現象とは、回路を流れる電流が定常状態になるまでに電流等がどういう振る舞いをするかを考えることです。
今回はRL回路でやります。頑張りましょう。
RL直列回路
以下に示すようなRL回路を考えます。ただし、抵抗の抵抗値をR、コイルの自己インダクタンスをLとして、回路を流れる電流をiとします。
回路を流れる電流の時間変化を求めます。
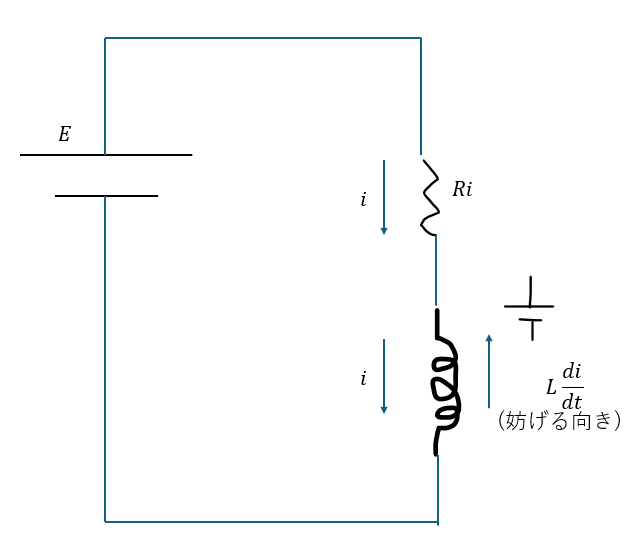
コイルに電流が流れると言うことで、コイルに下向きの磁束密度が増加します。これを妨げる向きに誘導起電力が発生します。
電流の向きに誘導起電力だけの電位降下が起きると思って回路の方程式を立てれば良いです。
電流の振る舞い
回路の方程式を立てて電流の振る舞いを時間の関数として表します。
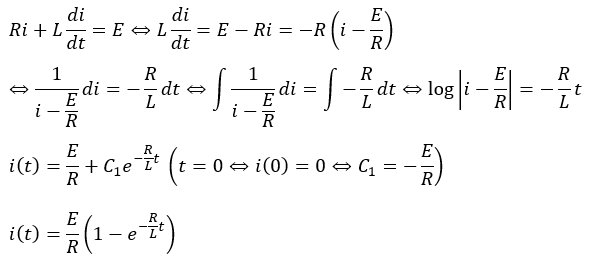
コイルに流れる電流について、以下のことが言えます。
- 流れる電流はE/Rになりたい
- けど、コイルに誘導起電力が生じて変化を妨げる
- だから、時間を掛けて流れる電流がE/Rになる
- 時間が経つとコイルは導線と見なせる
コンデンサとコイルに電流を流したときの違いをまとめます。
- コンデンサ
- t=0では導線と見なせる
- 時間が経って電荷がたまると電流は流れない
- コイル
- t=0では誘導起電力のせいで電流は流れない
- 時間が経つと電流が変化しなくなって導線と見なせる



コメント