こんにちは。Horyです。
今回は整数問題で紹介し忘れていたN進法による数の表記方法に関して簡単に解説します。
整数をN進数に直すことは誰でもできると思いますが、小数をN進数に直す問題は盲点になることが多いように感じますので、今回の記事ではそれらのことも詳細に解説します。
今回も頑張りましょう。
N進法
私たちが普段見る数字は10新法により記述されています。
どういうことかと言うと・・・
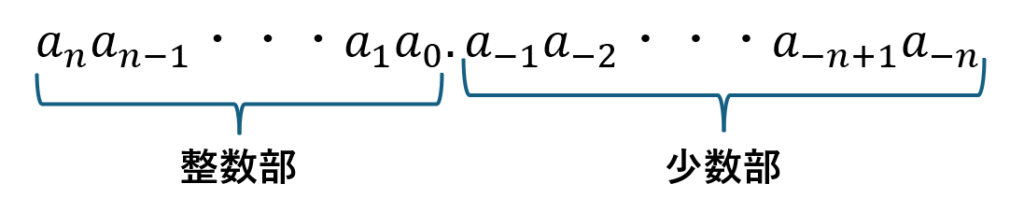

上のようなルールに従って数字を表記することを「10進法による数字の表記」と言います。
N進数による数字の表記は上のことの応用です。

このように表すことでN進法により数を表記できます。
数の表記方法
N進数による数の表記方法を説明します。
例えばですが、10進法で199と表されている数を2進法・4進法・5進法で表してみます。
重要なのは割り算をしたときの余りです。

N進数で記入したときはそのことが分かるように書き換えた数字の左に小さく(N)と書いてください。
10進法の場合、その必要はありません。
N進数を10進数に直すときは逆作業をすれば良いです。
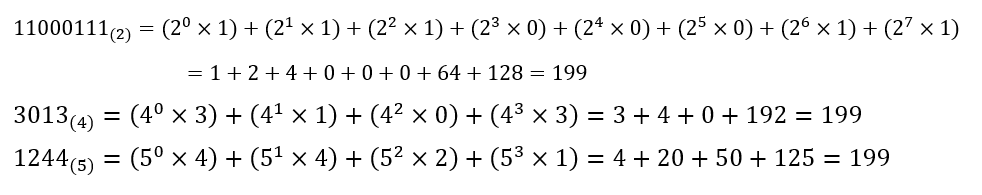
小数の表記方法
問題は小数をN進数で表記する場合です。
これはやり方を知らないと出来ないです。
例えば、10進数で以下のように表されている数字を2進数で表してみます。
各桁の数字は0か1のどちらかです。
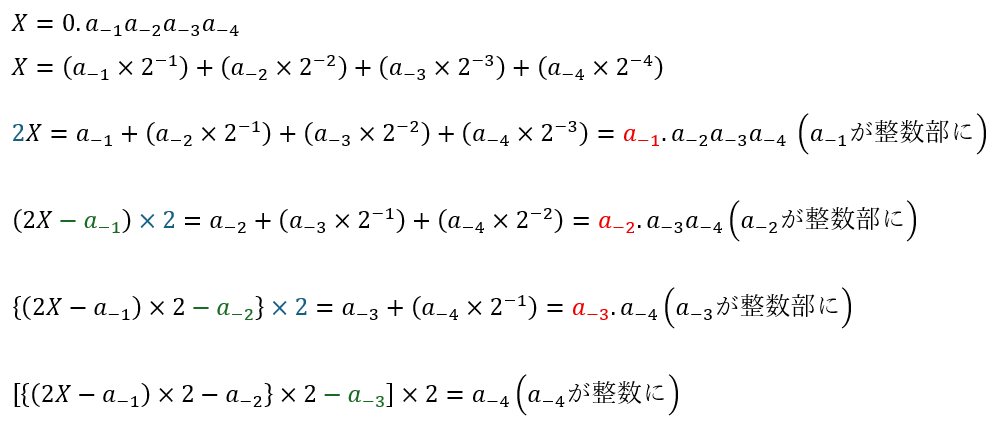
上に示すように2進数の場合、2を小数に掛けた結果の整数部を評価することで小数部の数字を導出します。
実際に実演してみます。
10進数で0.174と表されている数を2進法で途中まで表してみます。

上の図のように計算がめちゃくちゃ長くなるので最後まではやりません。
本当に求めようと思ったら、2を整数が現れるまで掛け算し続けます。
上の図で緑の斜線を引いた意味は計算式における緑の値を引いているという意味です。
また、図の赤い部分の意味は計算式における赤の値を出して各位での数字を求めたと言う意味です。
小数部のN進数の表記方法も覚えておきましょう。



コメント