こんにちは。Horyです。
今回の記事では半導体の基本について解説しようと思います。
半導体にはn型半導体とp型半導体が存在してこれらの違いについて説明すると共に、半導体の性質を応用した電子部品であるダイオードの整流作用に関しても原理から説明します。
今回も頑張りましょう。
半導体の性質
まずは、半導体の性質に関して簡単に解説します。
- 導体・・・電気を通す (金属)
- 絶縁体・・・電気を通さない (ゴムとか)
- 半導体・・・導体と絶縁体の性質持つ (電気を流したり流さなかったり)
半導体は特定の条件で電気を流す性質を持つ物質です(その条件でなければ電気を流さない)。

また、純粋な半導体に添加物を微量に投入して電気的特性をコントロールした半導体を不純物半導体と呼びます。
半導体に用いられる元素は13~15族が多いです。
- 13族元素・・・Al, Ga, In
- 14族元素・・・Si, Ge, Sn
- 15族元素・・・P, As, Sb
不純物半導体にはn型半導体とp型半導体があるので、これらの2つの性質を解説します。
n型半導体の性質
n型半導体の性質を手順に従って紹介します。
- 14族元素の純粋半導体 (Si)
- 15族元素が混入する (Sb)
- 15族元素の電子が1つ余る
- 電圧をかけることで余った電子が移動して電流が測定
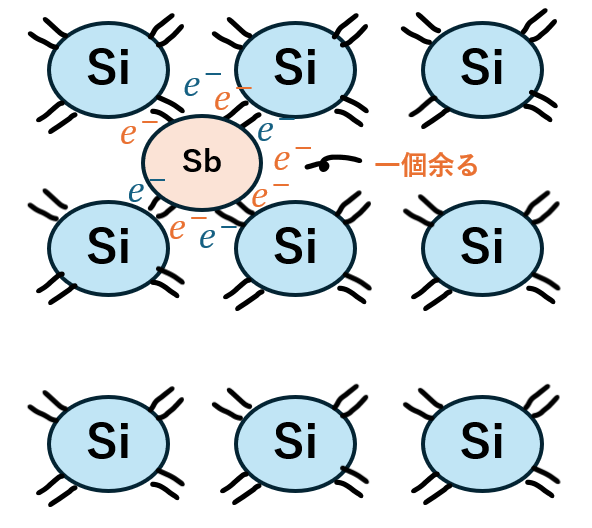
14族元素の最外殻電子が4個に対して15族元素は5個です。
共有電子対は4ペアできますが、15族の電子が1個だけ余ってしまいます。
余った一個の電子が電気伝導に寄与するわけです。
p型半導体の性質
p型半導体の性質を手順に従って紹介します。
- 14族元素の純粋半導体 (Si)
- 13族元素が混入する (In)
- 13族元素の電子が1つ足りなくなる
- 足りなくなった部分が空席となってこれを正孔(ホール)と言う
- ホールは正電荷のように振る舞う
- 電圧を加えるとホールは電流の向きに移動して電流が測定
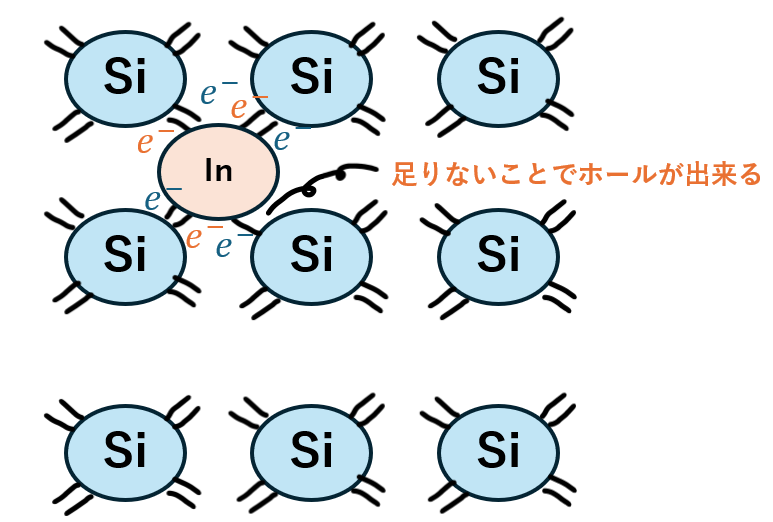
14族元素の最外殻電子が4個に対して13族元素は3個です。
共有電子対は3ペアできますが、13族の電子が1個だけ足りなくなります。
足りなくなった部分は正の電荷を持った孔と見なされ、これが電気伝導に寄与するわけです。
半導体ダイオードの性質
半導体ダイオードはn型とp型の半導体を組み合わせることで出来る電子部品です。
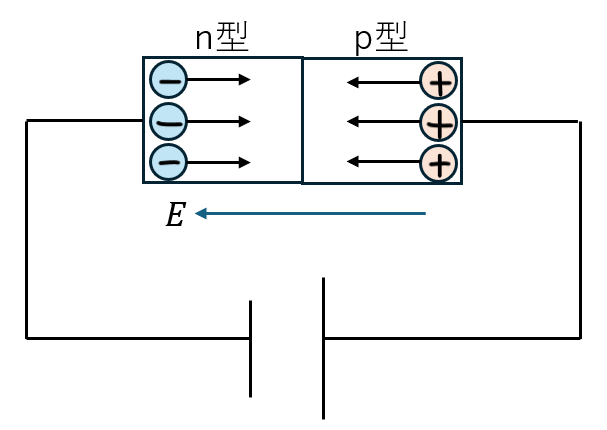
- 電圧をp型→n型の向きに流す (順方向)
- p型側・・・電場によって正孔が力を受けて中央に移動
- n型側・・・電場によって電子が力を受けて中央に移動
- 中央(接合面)で出会った電子とホールは正と負で消滅する
- 電流が流れる
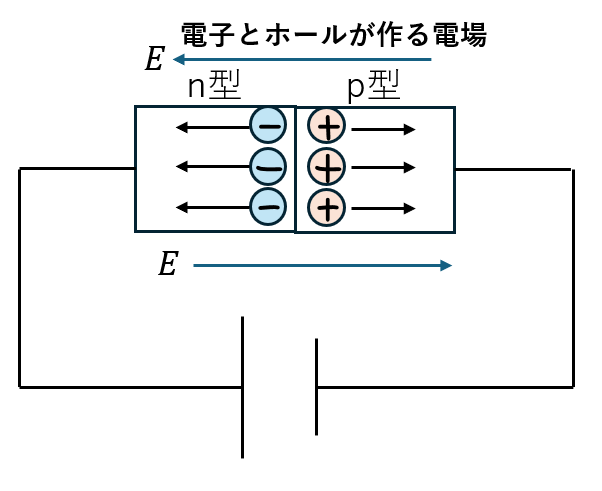
- 電圧をn型→p型の向きに流す (逆方向)
- p型側・・・電場によって正孔が力を受けて端部に移動
- n型側・・・電場によって電子が力を受けて端部に移動
- 端部の電子とホールで逆向きの電場を作る
- 電流が流れない
半導体ダイオードは電気回路では以下の記号に示すように記述します。
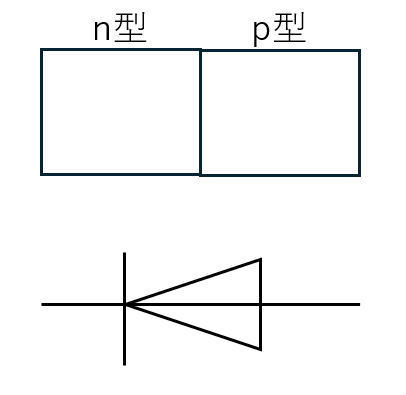
電圧をかける向きによって電流が流れるか・流れないかが決定されるダイオード特有の性質を整流作用と言います。
ダイオードの問題
ダイオードに関する簡単な問題を紹介します。
以下に示すような回路図を考えます。
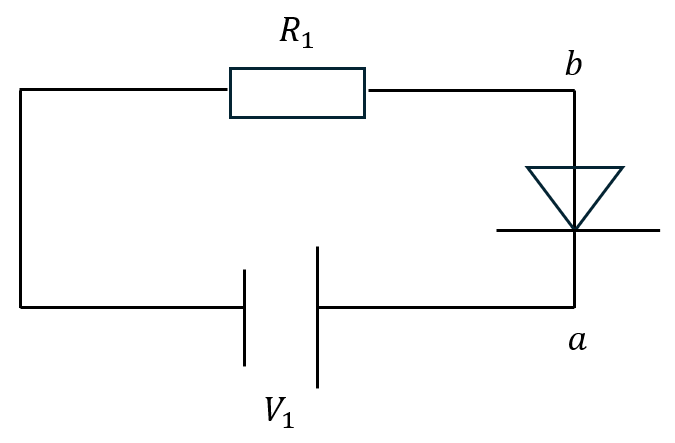
このような問題では回路に流れる電流を求めさせる問題が出ます。
- 回路に流れる電流;I
- ダイオードで消費する電圧;v
- 起電力;V1
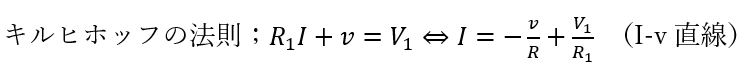
このままでは求められないと思うかもしれませんが安心してください。
問題には大抵の場合、ダイオードの電流-電圧曲線のグラフが出ます。
キルヒホッフの法則で導出したI-v直線をグラフ上に記述して導いた交点が電流の値になります。
上の問題の応用です。
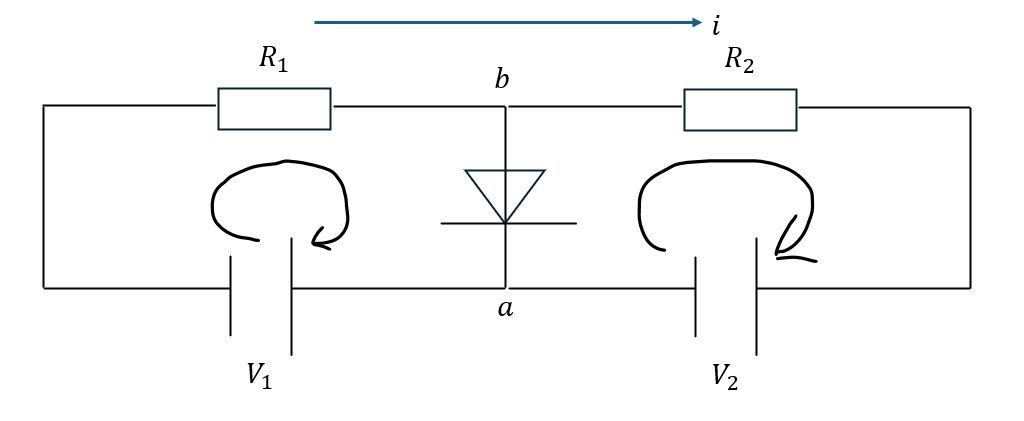
上の図ではダイオードに電流が流れないときの可変抵抗値R2の値を求めろとかの問題が出ます。
ダイオードに電流が流れないと言うことはb-a間は等電位になります。
キルヒホッフの法則を2つの閉回路で立てます。
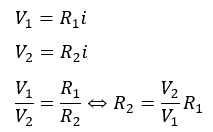
R1が定数と見ると、抵抗値R2を小さくすればするほどbの電位がaの電位よりも高電位になってダイオードの整流作用によりba間に電流は流れません。
ちなみに、電流の求め方は大回りでキルヒホッフの法則を立てると・・・
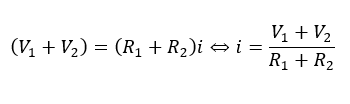



コメント