こんにちは。Horyです。
今回はe^πとπ^eの大小関係に関する問題を解いていきます。
かなり有名な問題なので必ずできるようになってほしいです。
今回も頑張りましょう。
大小関係に関する問題
以下に示すのはこの記事で取り組む問題です。

これらの問題を例に解説します。(3)に関しては前回の記事で触れています。
(1)解答・解説
(1)の解答・解説です。
グラフを描く手順通りにグラフを描きます。グラフの描き方はこちらの記事を読んでおいてください。
ステップ① 定義域の調査
まずは定義域の調査です。以下の二点に注目します。
- 分母≠0
- 真数条件
以上から定義域は「x>0」∧「x≠1」です。
ステップ③④ 微分と増減表
この関数に対称性や周期性はないのでステップ②は省略します。
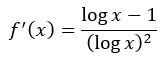
- 分母は必ず0より大きい
- 符号変化にかかわるのは分子のみ

ステップ⑤ 極限と漸近線
極限と漸近線を求めます。

ステップ⑥ グラフ
以下にグラフを示します。
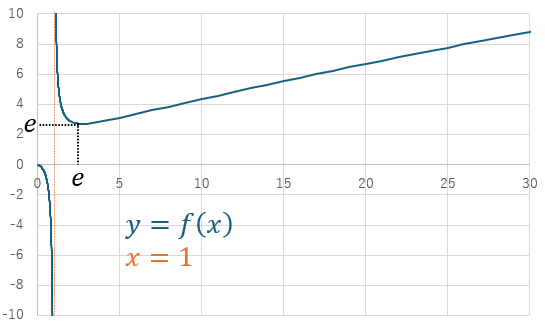
(2)解答・解説
(2)の解答・解説です。
グラフの描き方は手順通りに行いますが、定義域や極限・漸近線については省きます。
ステップ③④ 微分と増減表
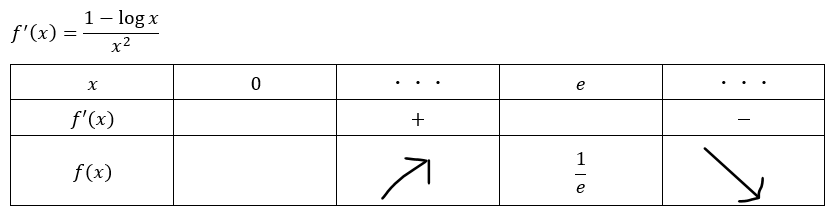
ステップ⑥ グラフ
以下にグラフを示します。
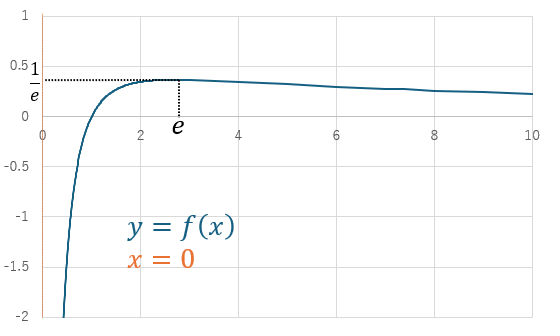
(3)解答・解説
方程式の解の数を調べる問題です。
ひとまず、肩にxが乗っているので両辺の対数を取りましょう。
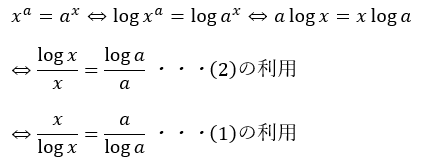
このように分離法が使えます。ただし、「y=a」の形ではないことに注意してください。aの値の変化で「log a/a」や「a/log a」がどのように推移するかをよく考えてください。
(1)のグラフを利用
(1)のグラフを利用する方法です。
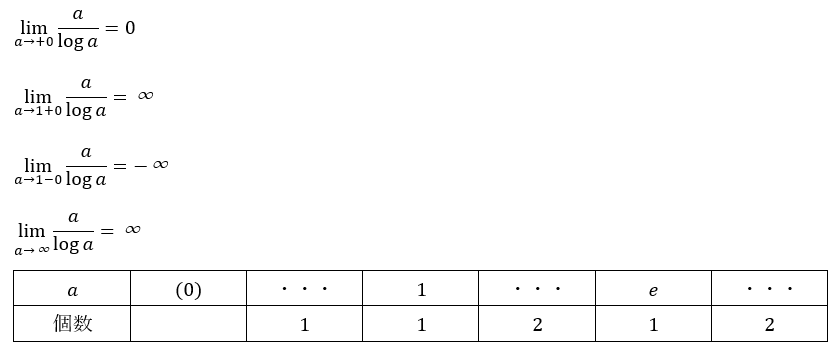
もし分かりにくければaに具体的な値を代入してみてください。
(2)のグラフを利用
(2)のグラフを利用する方法です。
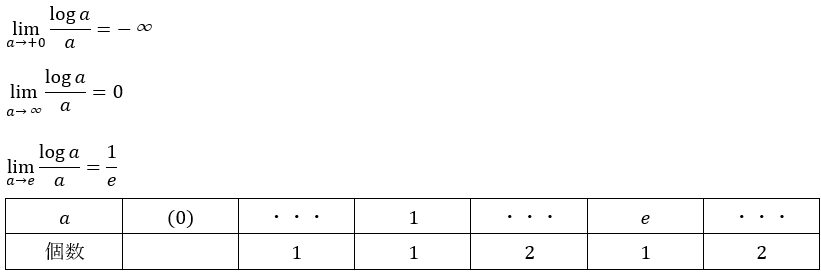
以上からどちらのグラフを使っても答えが同じになることが示されました。
(4)解答・解説
(2)のグラフを利用します。グラフから、求めた関数は「x>e」の範囲で減少するので、次の不等式が成立します。
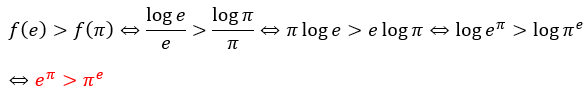
以上により大小関係を求めることができました。大小関係が判断しにくい数でもちょっとした工夫で求めることができます。これも数学の醍醐味の一つです。
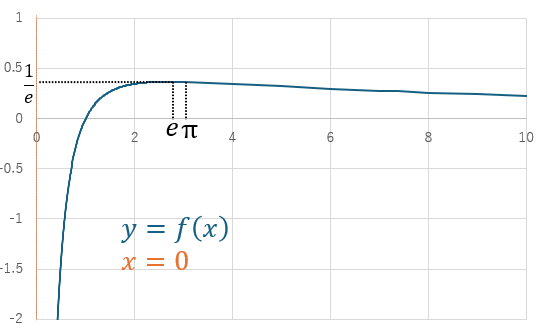



コメント