こんにちは。Horyです。
以前に二枚の色紙を重ねて回転させたときに重なる部分の面積を求めたりしました。
今回の記事では折り紙を折ったときに重なった部分の面積を求める問題を解説します。
今回も頑張りましょう。
折り紙と重なり
皆さんも折り紙を折ったことはあると思います。
以下の図形をご覧ください。
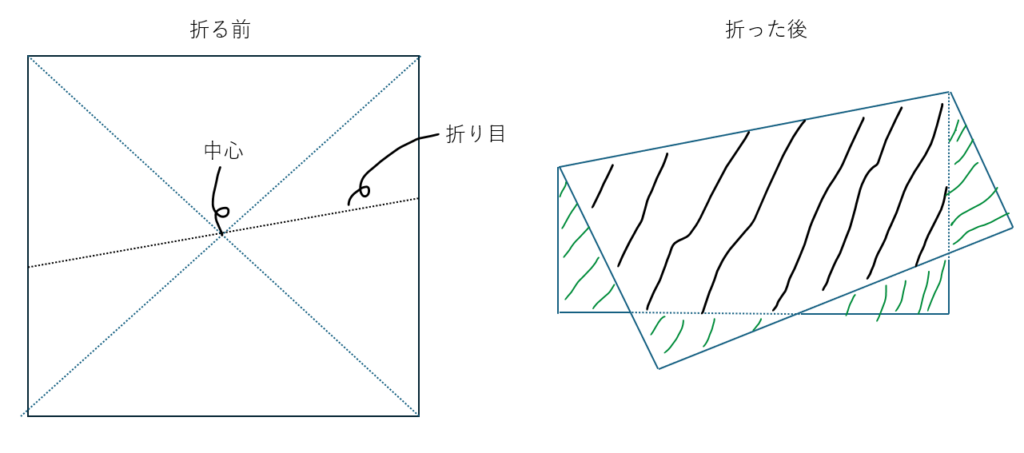
ルールを以下のように定めます。
- 折り紙は一辺が1の正方形
- 折り目は必ず折り紙の中心を通る
- 折った後の図形の斜線部の面積を求める
非常に良い問題になりますので頑張りましょう。
問題を解く前の下準備
まずは、問題を解く前の下準備です。
この問題のポイントですが、問題を「図形の折り返し」と見るか「図形の回転」と見るかで考え方が大きく変わります。

今回であれば回転で考えていきます。
辺or角のどちらを変数に取るかですが、正方形の一辺は1と分かっているので今回は角度を取ります。
また、図形の折り返しは折り返す前の図形の特性が残っているので相似を非常に利用しやすいです。
ちなみに、EOは正方形の対角線のため、○で表された角度は45°です。当たり前です。
角度に関して立式します。
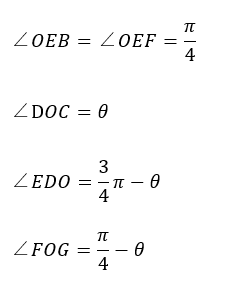
解答・解説
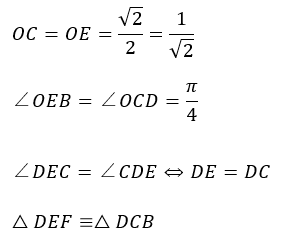
以上の議論からはみ出た直角三角形は全て合同です。
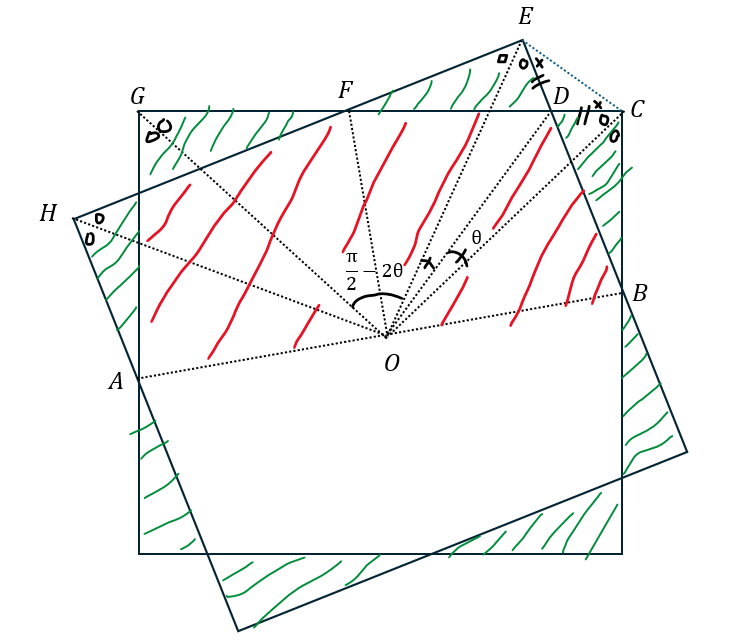
- 赤い部分・・・求めたい面積
- 緑の部分・・・はみ出た直角三角形
- 赤い面積=正方形の半分-直角三角形2個
以上からはみ出た直角三角形の底辺と高さを求めれば勝ちに近づきます。
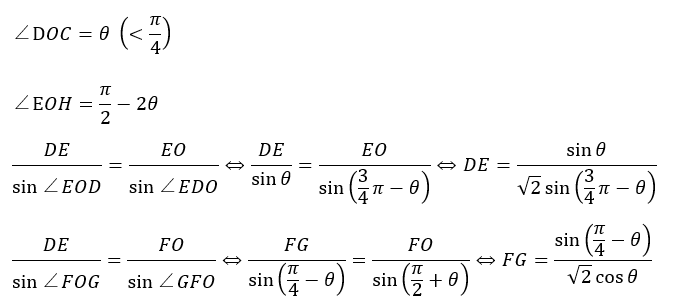
以上から題意の面積を求めることが可能です。
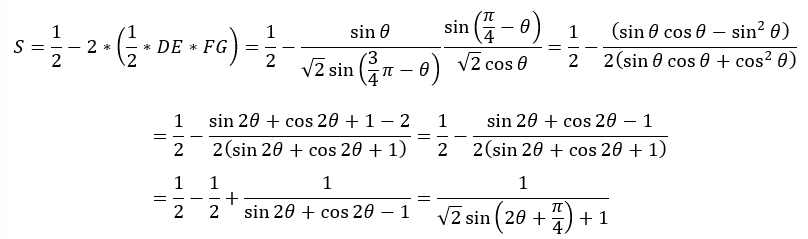
ここまで来たら最小値や最大値を求めてみてください。
余談;別解について
本問には様々な別解がありまあす。
- 計算方法;
- 分母と分子をcos^2θで割り算
- tanでSを表す
- 相加相乗平均
- 計算方法
- 分母と分子に「積⇒和の公式」
- 解答方法
- 回転とみて全ての点に座標を導入
- ベクトルと直線の方程式
- パワー数学
余裕のある人はやってみてほしいです。


コメント