こんにちは。Horyです。
前回の記事ではcosとその2倍角、3倍角の積を関数として最大値や最小値を求めました。
また、このような問題は予選・決勝法を用いて解いたこともあります。
今回の記事は問題としては上の記事の問題に似ているかもしれませんがやり方が少し異なる問題を紹介します。
今回も頑張りましょう。
“sin A sin B sin C”
以下はこの記事で解説する問題になります。
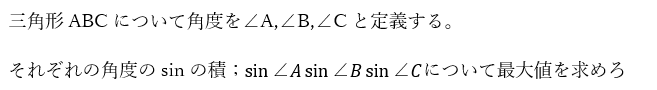
この問題を例に解説します。
前回の問題と大きな違いは角度に関連がないことです。
というのも、前回はx,2x,3xで角度を加法定理で合わせることが出来ましたが今回はそう上手くいきません。
どうしたモノかと思いますが、まずやるべきことは以下の2つです。
- 角度を1つ減らす
- 条件を自分で追加する
角度を1つ減らす
以下の記事でも紹介しましたが、三角形であれば角度を1つ減らせます。
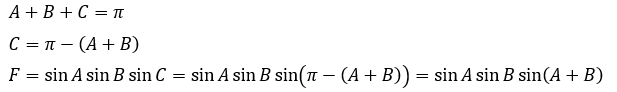
このように角度を1つ減らせました。
自分で条件を追加する
数学が出来ないやつは闇雲にやろうとします(そういうのを僕はパワー数学と呼んでいて効果的な時もある)。
ただ、そのような方法は非効率です。
今回であれば各sinの文字は等しいです。
そのため、「∠A <∠B <∠C」としても差し支えないです。
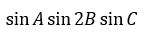
上に示すような場合で一般化は出来ません。
sinの角度が均等でなければこの方法は用いることが出来ません。
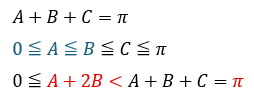
何で上の赤い式を登場させたかというと、上でA,Bだけの式にしたために、角度A,Bの条件式を増やしたいと考えるからです。
また、上の不等式から最小の∠Aについて、A≦60°であることが分かります。
これは考えれば当たり前ですが、60°を超えると残りの角度でBとCを等分したときにBがAより必ず小さくなります。
∠Aの固定
皆さんは予選・決勝法を覚えていますでしょうか?
最小の角度A(0°~60°)の範囲で固定して∠Bを動かします。

また、3つのsinの積になっているのが非常にやりにくいので「3つのsinの積」から「sinとcosの積の和」に変形します。
積⇒和の公式が使えそうですね!
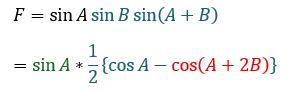
ここで、Aの範囲から上の緑の部分は正です。
Aは固定されているので上の赤い部分のみで最小値を考えましょう。
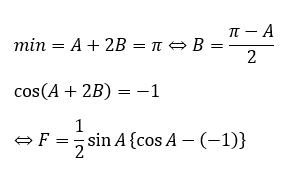
予選での最大値で∠Aを動かす (微分その1)
∠Aを0°~60°の範囲で動かして最大値の最大値を求めます。
ここまで来れば微分を用いるだけです。
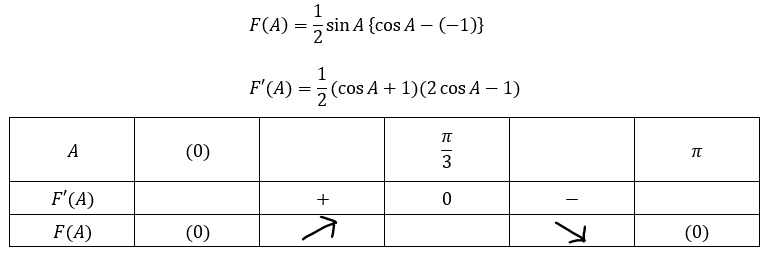
以上から最大値は角Aが60°になるときで、このとき、角Bも60°になるのでABCが正三角形になるときに最大値を取ります。
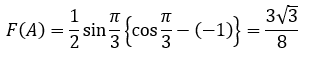
予選での最大値で∠Aを動かす (微分その2)
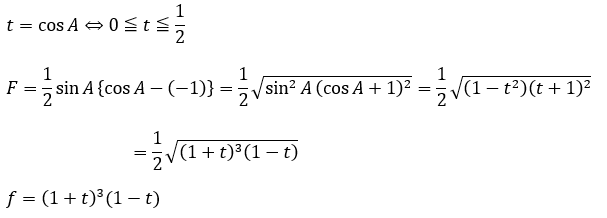
要は、ルートの中身がどうなっているかなので、ルートの中身を展開した多項式関数を微分すれば答えが出ます。


コメント