こんにちは。Horyです。
これまでは三角比を用いた図形問題を解説してきました。
今回の記事から三角関数の最大値・最小値に関して応用問題を解説します。
かなり前の記事になりますが三角関数で最大値や最小値を求める時の定石は話していますので良かったら読んでおいてください。
今回も頑張りましょう。
“cos x cos 2x cos 3x”
早速になりますが問題になります。
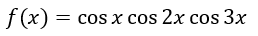
上に示す関数の最大値と最小値を求めろ。
前回の記事でも解説しましたが、三角関数の基本は以下の4つです。
- sin か cosに統一する
- 単位円の方程式
- 三角関数の合成
- 加法定理
- 次数下げ
- 半角の公式
- 角度の統一
- 半角の公式
- 加法定理
- 和と積の利用
- Sinθ+cosθ=t (和)
- Sinθcosθ=? (積_tで表す)
今回であれば、すでにcosで統一されています。
そのため、角度を揃える必要がありそうです。
角度を揃える
角度が2x, 3xとバラバラなので全てxに統一します。
チェビシェフの多項式でも話しましたが、cos nθは全てcosθの多項式で表せます。
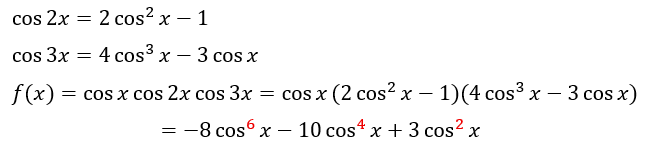
関数を解析する
数学が出来ないやつはcos xをtと置きます。
数学が出来るやつはcos^2 xをtで置きます(0≦t≦1)。
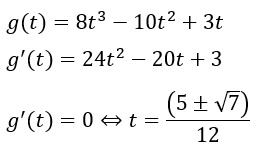
増減表を書いてみます。

極値の値を求めたいですが、数学が出来ないやつはg(t)に直接代入しようとします。
数学が出来るやつはg(t)をg’(t)で割り算します。
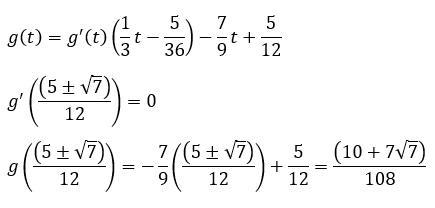
グラフの概形は以下の通りです。
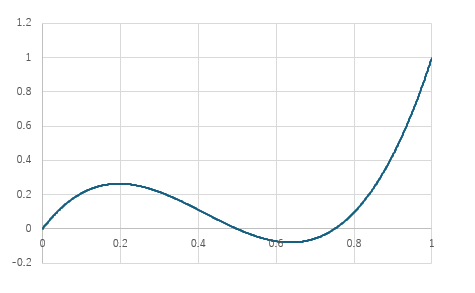
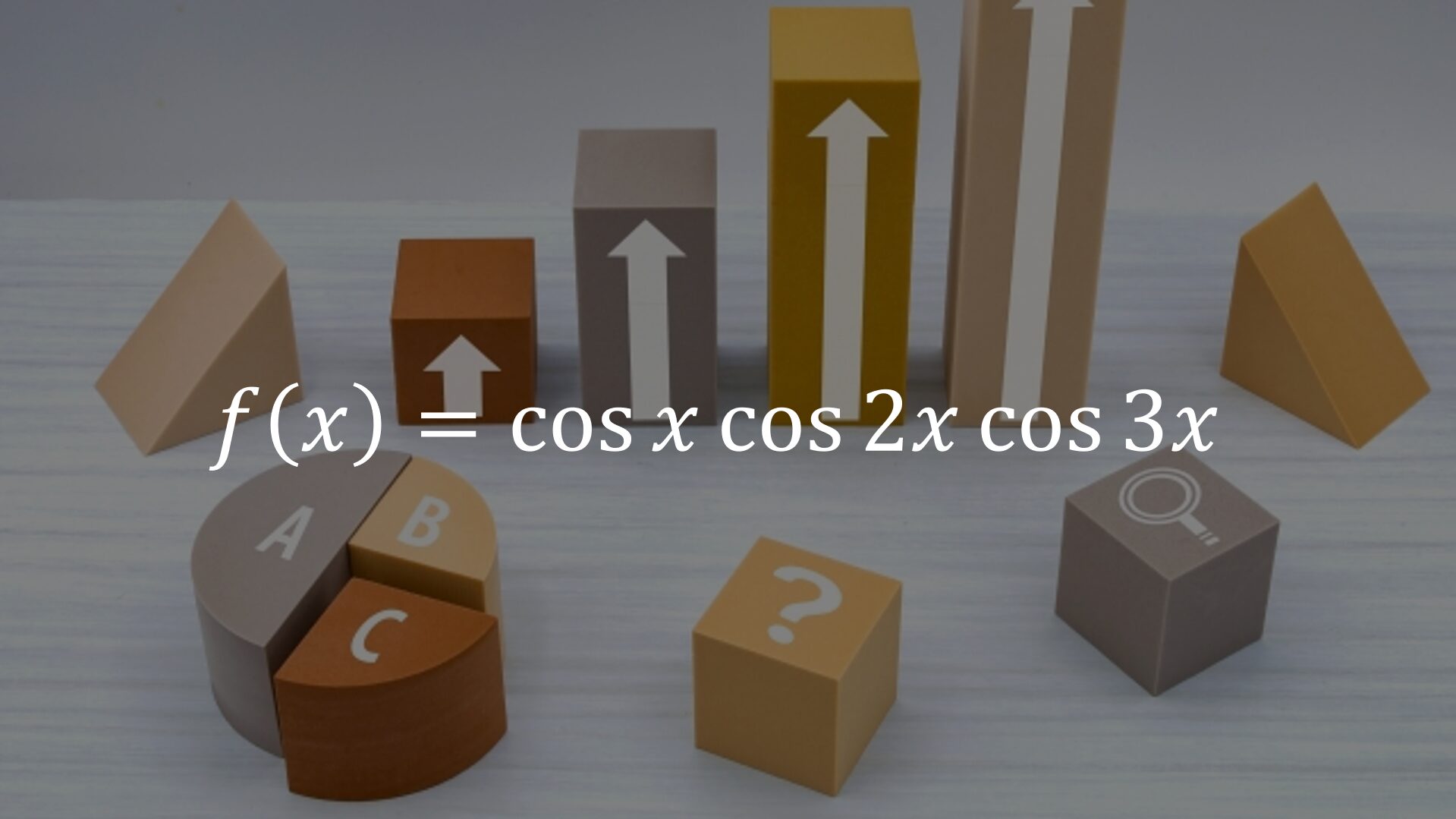


コメント