こんにちは。Horyです。
最近の記事で三角関数の等式や不等式について様々な問題を解説しました。
- 2つのsinの積と不等式 積⇒和の公式
- 三角関数の不等式と予選・決勝法
- sinの和とsinの積 「和⇒積」公式の複数利用
- 「tan A+tan B+tan C = tan A tan B tan C」 tanの和と積の公式
上で紹介した記事は角度に関する記事ばかりで辺と角度が関係する問題はありませんでした。
今回の記事ではそのような問題に取り組みます。
頑張りましょう。
辺と角の不等式
以下に示すのは辺と角の不等式に関する問題です。
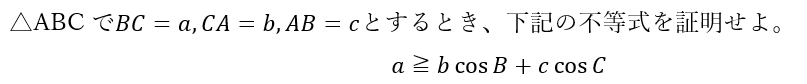
この問題を解説します。
辺と角が入り交じっています。 こんな時の処理方法は・・・
- 辺のみに統一する
- 角のみの統一する
2つの方法に関して個別に紹介します。
辺への統一
辺へ統一するためにcos を余弦定理で排除します。
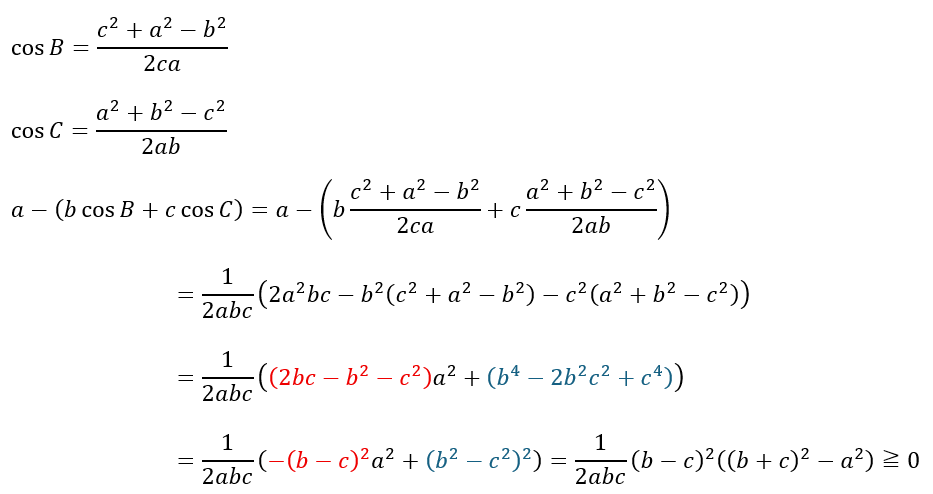
何で上の引き算が0以上になるの?
と疑問に思う人もいるかもしれませんが、皆さんは三角形の成立条件に関して覚えていますでしょうか?
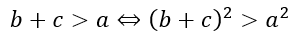
以上から不等式は成立します。
角への統一
角度に統一するために辺を正弦定理で排除します。
角度を出したくないので外接円の半径をRとします。
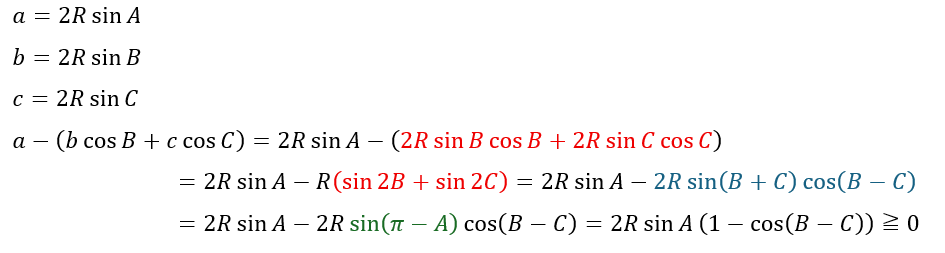
- 赤い部分;sinの倍角公式
- 赤⇒青;和⇒積の公式
緑の部分ですが、三角形で2角の和が出てきたら1つの角度で表せます。
これは覚えといた方が良いです。
sinの和と2倍角の和
角に関する不等式
上の不等式を応用して以下の不等式を証明してみましょう。
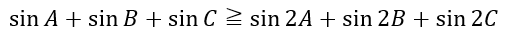
すでに角に統一されているので角のママやっていきます。
最初に証明した不等式をそのまま利用します。
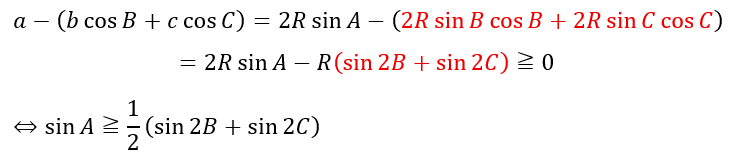
同様のことがsin Bやsin Cでも言えます。
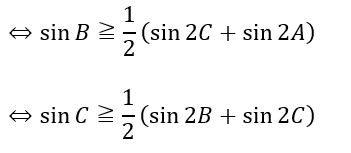
これらの3辺を合計すると・・・
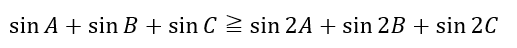



コメント