こんにちは。horyです。
前回の2つの記事でsinに関する不等式について紹介しました。
上の記事は「積⇒和」を利用した方法を用いていましたが「和⇒積」の公式もあります。
そして、多くの学生は「積⇒和」はできるものの、「和⇒積」は出来ない人が多いです。
今回はそんな「和⇒積」の公式を多用する不等式の証明問題に取り組みます。
今回も頑張りましょう。
sinの和とsinの積
sinの和と積に関する不等式を証明します。
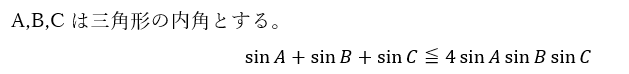
この不等式を証明します。
ちなみに、これに似たtanの等式証明は前回の記事でやりましたね。
具体的に何をどうして良いか分からないと思いますが・・・
- 左辺が和で右辺が積
- どっちかに統一したい
- 積に統一するために和積公式
- 和関公式で角度が変わる
- 角度も統一したい
前回の記事でも紹介しましたが、「和⇒積」「積⇒和」を用いるのは・・・
- 和か積のどちらかで統一したい (両辺とも同じ形にしたい)
- 和⇒積にすることで共通因数で括れる
- 和⇒積や積⇒和にすることで項が消える場合がアル
解答・解説
左辺を変形します。とにかく掛け算の式に変形したいです。
色がついた部分は和⇒積の公式を使っています。
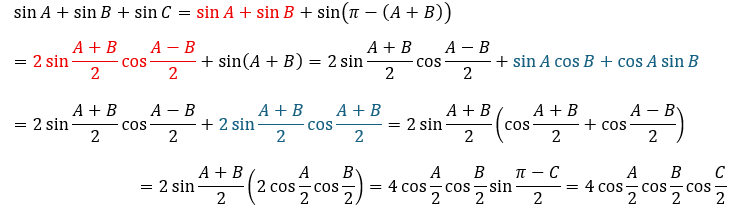
これにより左辺は完成しました。
一方で右辺は積の形にはなっていますが、1/2倍角を登場させたいのでsinの倍角公式を利用します。
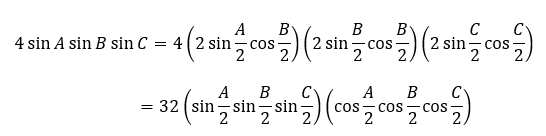
これで右辺も完成しました。
左辺から右辺を引き算します。
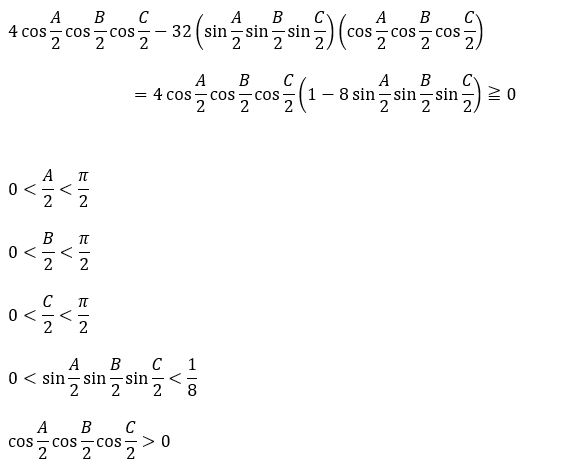
ちなみに、sinの積の範囲に関しては前回の不等式をそのまま利用しています。
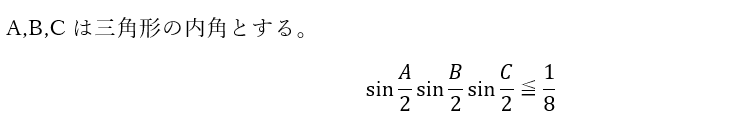
以上により不等式を示せました。


コメント