こんにちは。horyです。
皆さんは多変数関数の最大値・最小値を求める方法で予選・決勝法という方法をご存じでしょうか?
だいぶ昔になりますが、本ブログでも紹介しました。
多項式関数で予選決勝法は見たことがあるかもしれませんが三角関数で見ることは少ないのではないのでしょうか?
今回はそんな問題に挑みます。
今回も頑張りましょう。
三角関数の不等式と予選・決勝法
不等式に関する問題です。
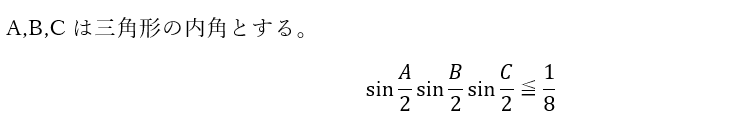
この問題は3つのsinの積です。
- 文字を1つ減らす (AとBだけにする)
- 積⇒和の利用
また、右辺が唯の数字なので左辺を関数と見てしまいましょう。
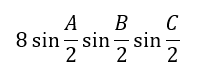
上の式に示す量の最大値が1であることが証明できれば勝利です。
2文字化+積和
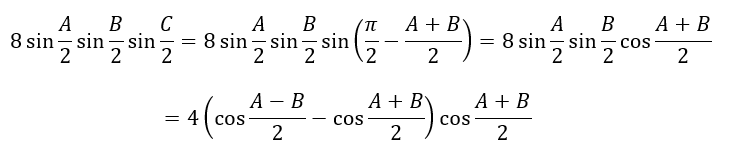
積和の公式はこちらの記事です。
積⇒和は誰でも出来ます(和⇒積が出来ない人が非常に多い)。
ここで、文字を簡略化します。

予選・決勝法
文字の範囲を決めます。
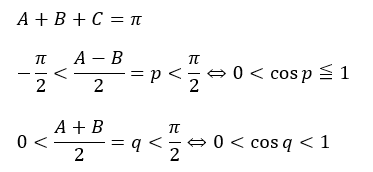
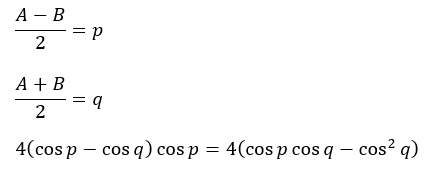
- cos pの次数;1次
- cos qの次数;2次
難しい方を固定したいのでcos qの方を先に固定します。
すると、この関数はcos pに関する一次関数となります。
また、qの範囲からcos qは正の数なので右上がりの直線です。
従って本直線の最大値は・・・
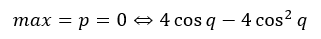
予選が終わったので決勝戦です。
qを動かして最大値の最大値を求めます。
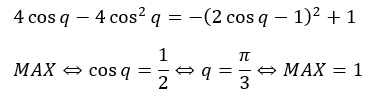
以上から最大値が1になったので左辺が1以下になることが示せました。
最大値の時の三角形の形状
ちなみに、最大値の時の三角形の形状は。。。
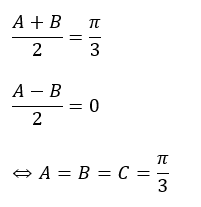
以上から最大値のとき、三角形ABCは正三角形です。
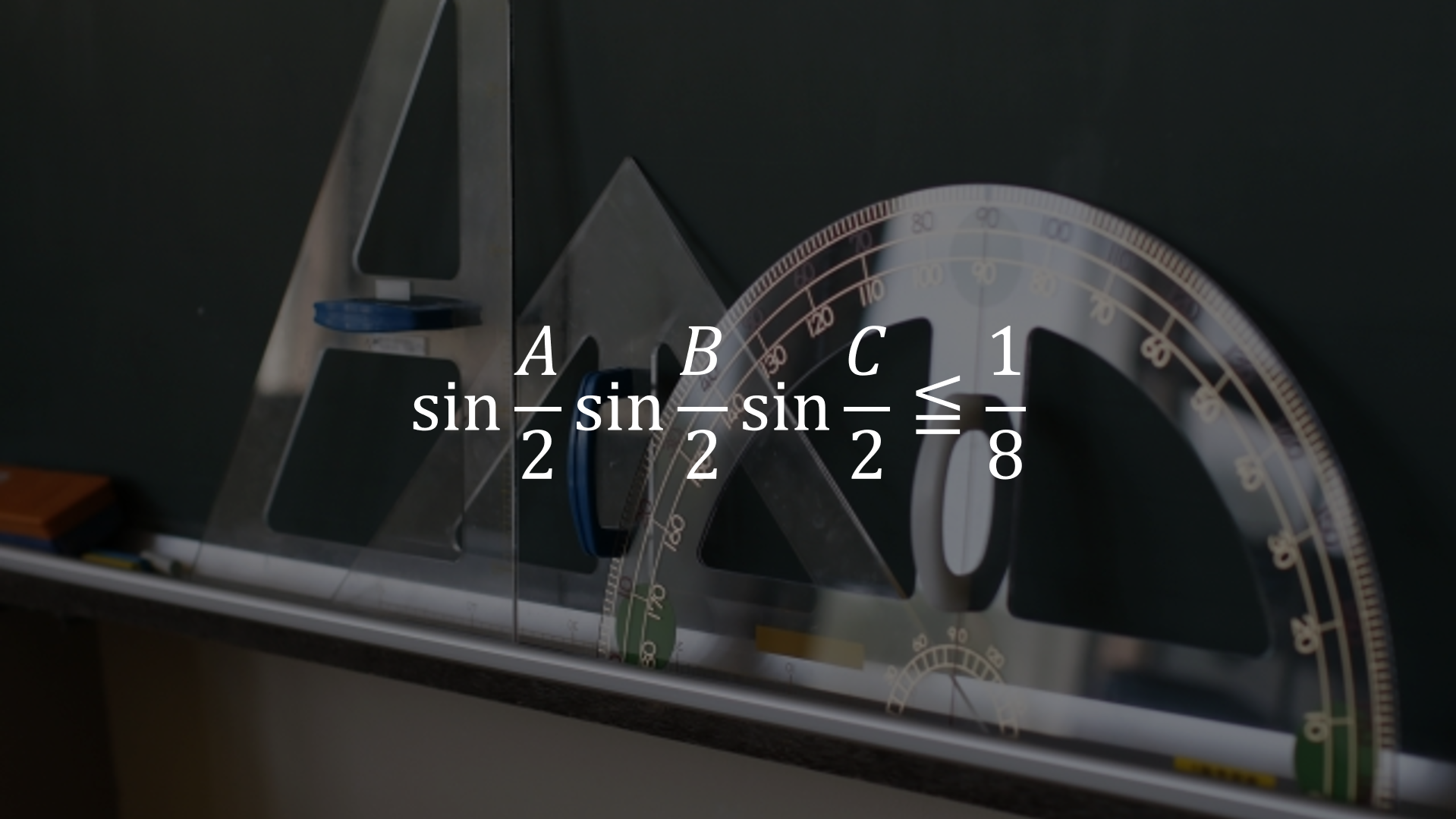


コメント