こんにちは。Horyです。
私たちはこれまでに数学ⅠAⅡBを用いる様々な図形問題に取り組んできました。
今回の記事では体積と表面積が等しい円柱が他に作れないような条件を求める問題に取り組みます。
今回も頑張りましょう。
唯一の直円柱
以下に示すのは問題です。

この問題に取り組みます。
問題文の意味について説明します。
- 直円柱の底面半径と高さを特定の値にする (直円柱①)
- 底面半径や高さを変える
- 直円柱①と体積・表面積が同じ直円柱はできない
このような半径と高さを求める問題になります。
問題を解く前の下準備
小学校で習った知識ですが円柱の体積や表面積について求めておきます。
(特に側面積に関しては忘れる人が多い)

直円柱①の体積と全表面積を求めます。
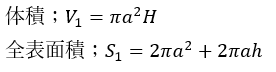
側面積が分からなくなったときは展開式を考えてみてください(図形問題で展開図を考えて二次元化するのは有効なときがある)。
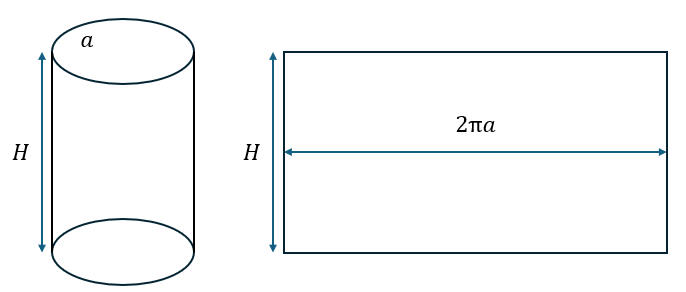
事前準備も終わったので解答・解説に移ります。
解答・解説
解答・解説に移ります。

直円柱①と②の体積と全表面積が等しいです。
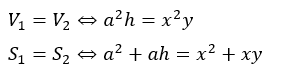
体積の関係式からyをxの式で表します。
これを全表面積の式に代入することでxに関する二次方程式が完成します。

- 赤い部分・・・半径がaで高さがhの条件
- 青い部分・・・大切
青い部分が非常に大切です。
青い部分がx=aのみを解に持つ条件を考えます(x>0の条件下で)。

xは0以上であることが条件なのでx=-2aは答えになりません。
そのため、高さが半径の2倍の時が条件になります。
ここで、終わってはいけません。
そのような条件は他にもあります。それは、f(x)の判別式が0より小さくなる時です。
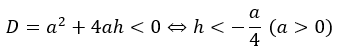
そもそも、hは0より大きいので、判別式の条件は不適当です。
こういったことに気付けるか気づけないかが明暗を分けます。
別解;微分を用いる
数Ⅲの微分を用いる方法を紹介します。
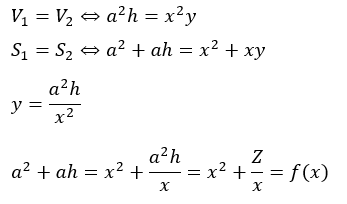
ここで、Zは定数と見なしています。

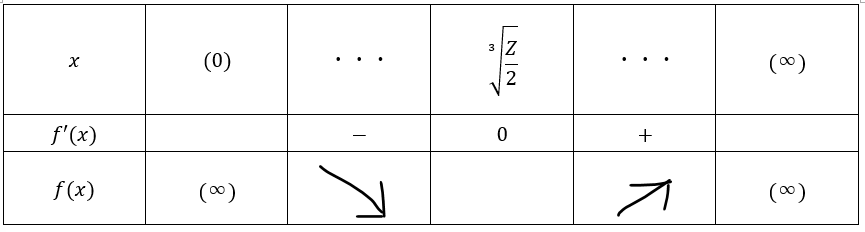
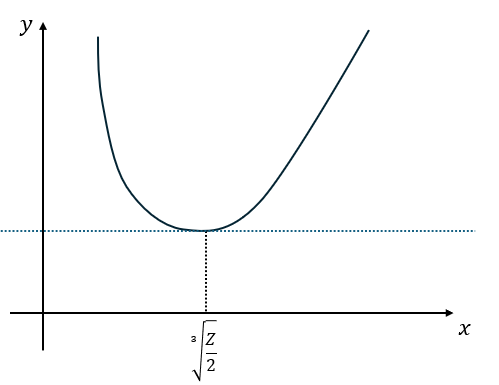
定数分離法により解が一つになればいいです。
今回であれば、上の図の点線を引いたところです(共有点が一つになると解を1つだけ持っていて、その解がaになればいい)。
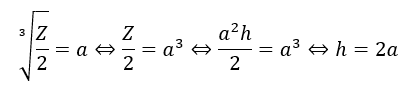
条件を求めることができました。



コメント