「f(f(x))－x」が「f(x)－x」で割り切れることの証明

こんにちは。Horyです。

これまでに整式の割り算に関する問題には多数取り組んだと思います。

今回は応用問題に取り組みます。

難関大でかなり出てくるような印象を受けるので今回も頑張りましょう。

「f(f(x))－x」が「f(x)－x」で割り切れる

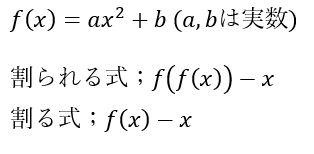
割り算を実行したときに割った余りが0になることを証明します。

ところで、整式の割り算のポイントを覚えているでしょうか？

①と②は皆さんが良く思いつくやり方ですが、③に関しては思いつかない人が多いです。

今回の問題は③を用いる問題です。

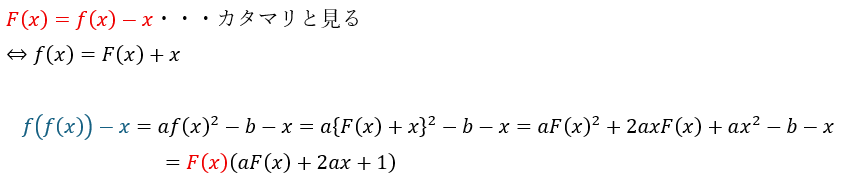
上の式の赤い部分を見てほしいです。

割られる式(青い部分)が割る式(赤い部分)を因数として持つことが分かりました。

以上から割り切れます。

この問題は問題そのものを暗記してもいいレベルの問題です。

上の問題のような形でなく、任意の多項式であったとしてもf(f(x))－xはf(x)－xで割り切れます。

二項定理をよく考えてください。

結局、因数にF(x)を持つので割り切れます。

折角なので実数解の個数に関しても考察してみましょう。

(1)で証明したことを最大限に利用します。

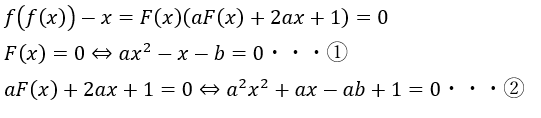
実数解の個数は①と②の二次方程式をうまく処理することで判断できそうですね。

注意すべき点は以下の二つです。

共通解を持つ条件は意外にも簡単です。

F(x)の取り巻きである2ax+1が0になれば②の解は①と一致します。

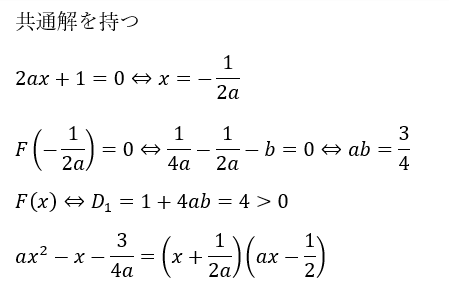
以上から共通解を持つとき、判別式は0より大きくなるので異なる二つの実数解を持ちます。

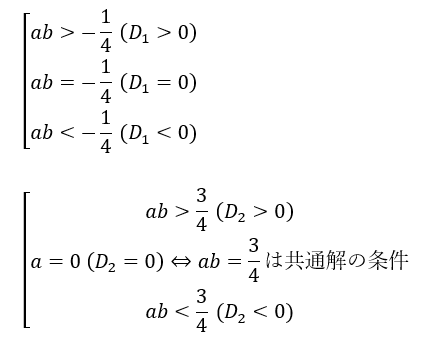
上の式①と②の判別式の条件を考えることで共通解を持たない場合の実数解の個数は議論できます(後は自習にします)。

先ほどの問題でカタマリの置き方を変えてみましょう。

上の二つは対称的な連立方程式になっていますね。

式が複数あって対称的になっていれば足し算・引き算 (掛け算)が強いです。

実数解の個数は上のy＝f(x)とx＝f(y)の二つの方程式を考えればいいですね。

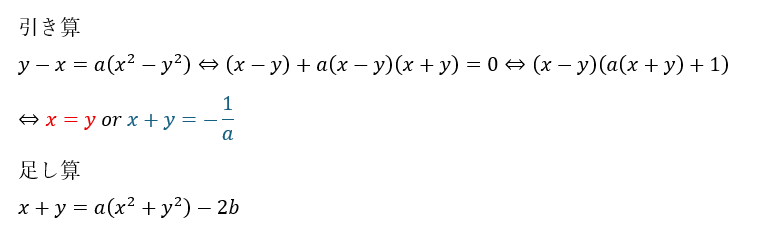
引き算で出てきた赤と青の二つの条件を足し算の式に代入すれば二つの二次方程式が出てきます。