こんにちは。Horyです。
自然数の中から異なる数字を選ぶ問題はありますが、2つの数字を選ぶ問題はあっても3つの数字を選ぶ問題はなかなかないと思います。
今回はそんな問題に取り組もうと思います。
頑張りましょう。
異なる3数の取り出し方
以下に示すのは異なる3数の取り出し方に関する問題です。

この問題を例に取り組みます。
簡単そうに見えます(実際にスッと解答できる)が意外とペンが止まる問題になります。
実験してみる
こういった問題は簡単な数で実験するのが吉です。
仮に最小の数であるn=6で実験してみます。
小さい数から当てはめてみると・・・
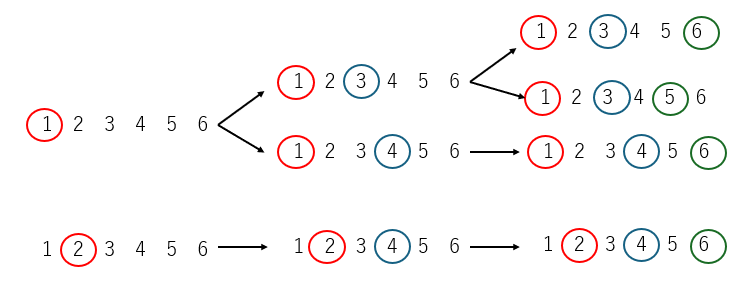
n=6のときは場合の数の総数は4つになります。
何かしら上手いこと不等式を作ると突破口が見えてきそうです。
解答・解説
解答・解説です。
1からnまでの整数の内の3つを小さい順からx,y,zと置きます。
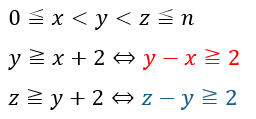
- 青い不等式からyを絞り込みます。
- yの最小値・・・y=3 (x=1でxの最小値)
- yの最大値・・・y=n-2 (z=nでzの最大値)
だったら、仮にy=kの時のxとzの数を考察してみればいいです。
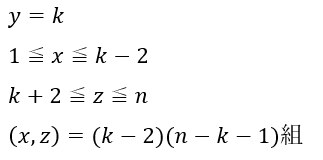
この組を全てのkに関して足し合わせれば勝利です。
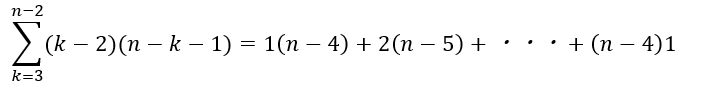
ここで、k=3からn-2というのが厄介なので、1からにしてみます。
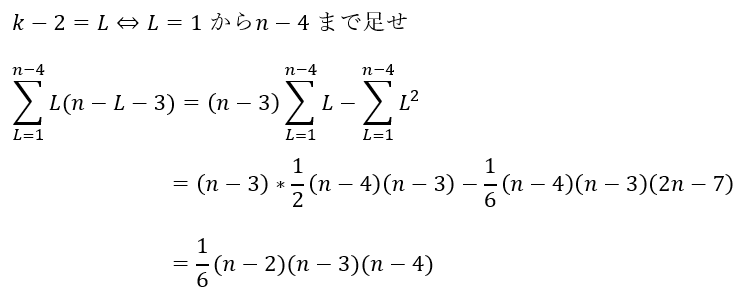
これって、1からn-2までの数字から異なる3整数を選ぶ場合の数と同じですね!



コメント