確率の問題でΣを用いることはよくあるかと思います。
Σを一回だけ使う確率の問題はあるかと思いますが、2回使う問題はなかなかないと思います。
今回の記事ではそのような問題を解説しようと思います。
今回も頑張りましょう。
Σを2回使う確率
以下に示すのはこの記事で紹介するΣを2回用いる問題です。

この問題を例に解説します。
ちょっと図に描いてみます(確率や漸化式では以下のように状況の推移を樹形図や絵に描くのが効果的)。
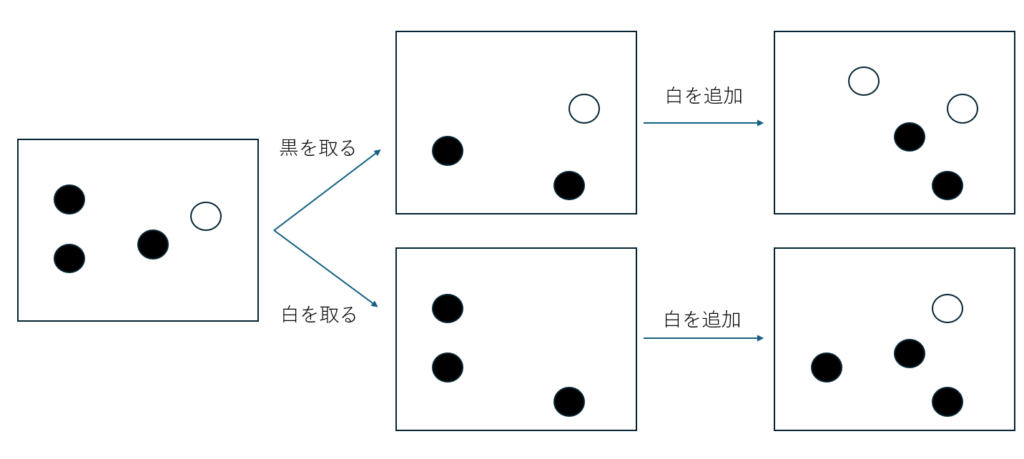
- 黒を取る⇒箱の中の白の割合が増える
- 白を取る⇒箱の中の状況は変わらない
(1)解答・解説
この問題は是非、解答してもらいたいところですね。
操作を繰り返した後に黒石が4個残っているということは箱の中の状況が最初と変わっていないということです。
つまり、白石だけ取られればいいということです。
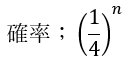
(2)解答・解説
n回繰り返した後に黒石が3つ残っているということはn回の操作までに黒石が1回だけ取られればいいということを意味します。
黒石がどこで取られるかが重要です。
以下では仮にk回目で黒石が取られるとしてn回の操作後に黒石が3つ残っている確率を考えます。

- 赤文字・・・1回目からk-1回目まで白石が連続して取られる
- 青文字・・・k回目に黒石が取られる
- 緑文字・・・k+1回目からn回目まで白石が連続して取られる
上で求めたkをk=1~nまで足しあげたものが求める確率です。

(3)解答・解説
この問題も(2)と同様の手法を用いますがちょっとめんどくさいです(Σを2回用いる)。
- k回目に最初の黒石が取り出される (1≦k<L)
- L回目に二回目の黒石が取り出される (k+1≦L≦n)
上の確率を求めていこうと思います。

- 求める確率について
- kを1からn-1まで足しあげる
- Lをk+1からnまで足しあげる
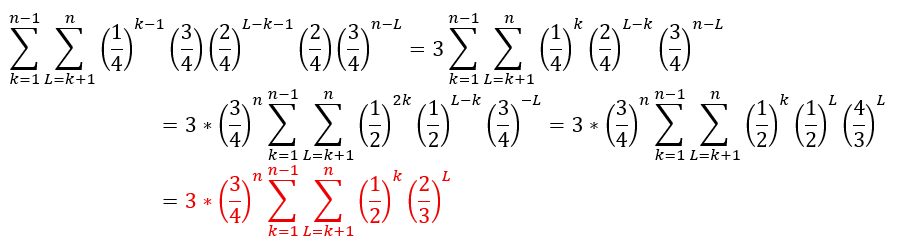
上の赤い部分を定義通りに計算していきます(計算地獄)。
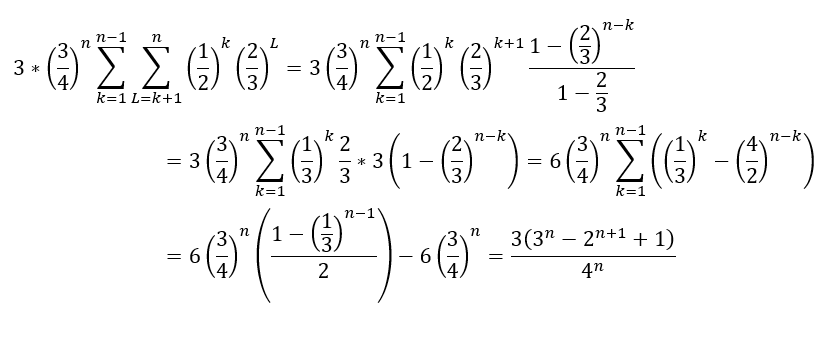
手順としては以下の通りです。
- 初めに文字が起点が文字(今回ならL)になるのΣを処理する
- 初めのΣを処理して導出できた式にkがある
- 元の式に合ったkのしきとまとめて後ろのΣを処理する



コメント