こんにちは。Horyです。
今回の記事では座標平面を用いる確率に関しての攻略記事です。
以前の記事では格子点を用いる確率の記事を書きましたが、それとは内容が全く異なります。
どちらかというと、数直線を動く点に関する確率の応用問題です。
今回も頑張りましょう。
座標平面を用いる確率
以下に示すのは本記事で取り組む座標平面を用いる確率についての問題です。

(1)については普通に数直線上を動く確率なので座標と試行回数に関する方程式を立てて求めたいですね。
一方で、(2)~(4)については(1)のように単純に方程式を立てても解けません。
何故なら、条件が非常に多く、方程式を立てるにしても大量に立てなければならないからです。
こんな時は、横軸を回数・縦軸を位置とする座標平面を作って考えるのが効果的です。
(1)解答・解説
- 4,6の目が出る回数・・・x
- 上記以外の目が出る回数・・・y
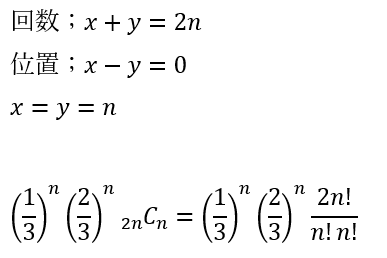
(2)解答・解説
- 横軸;回数に関する軸
- 縦軸;位置に関する軸
上のように軸を取って座標平面を記述してみます。
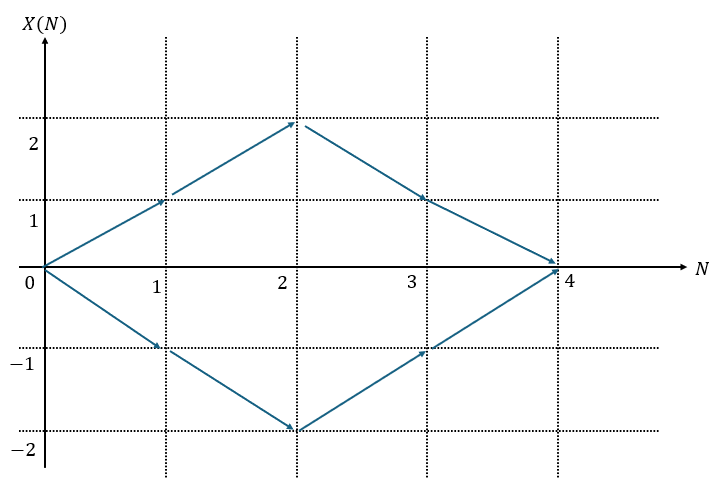
- 右上がりの矢印;4,6の目が出る
- 右下がりの矢印;4,6の目以外が出る
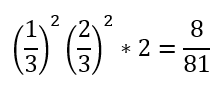
(3)解答・解説
これも(2)と同様に考えますが、少し複雑になります。
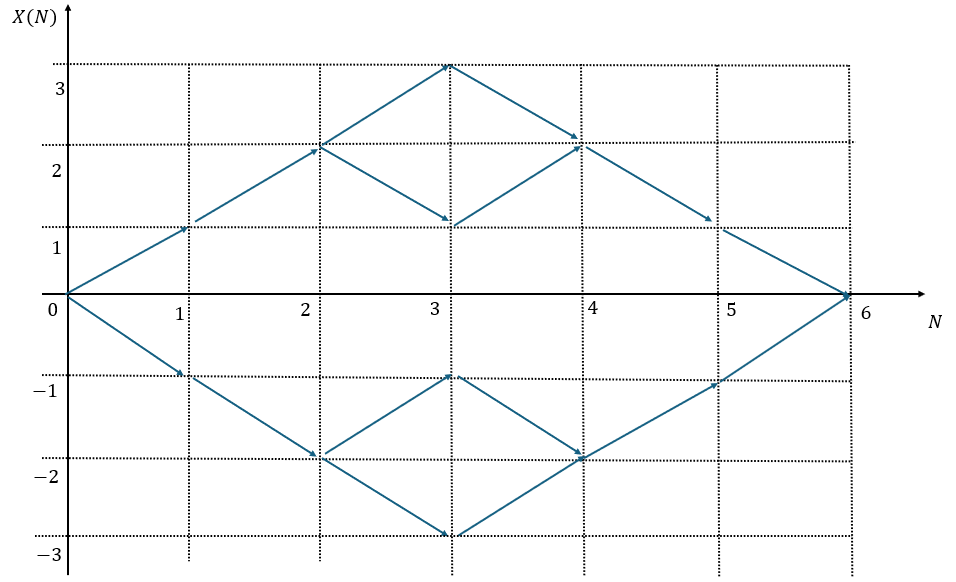
上の図を見ると移動の仕方は4通りあるので・・・
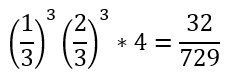
(4)解答・解説
これも(3)と同様の方法を行いますが、ここまで問題を解いてきた皆さんであれば察している人もいるのではないでしょうか?
これまでに書いてきた図形が横軸(回数軸)に対称であるということに・・・
これを意識して座標平面を記述すると・・・
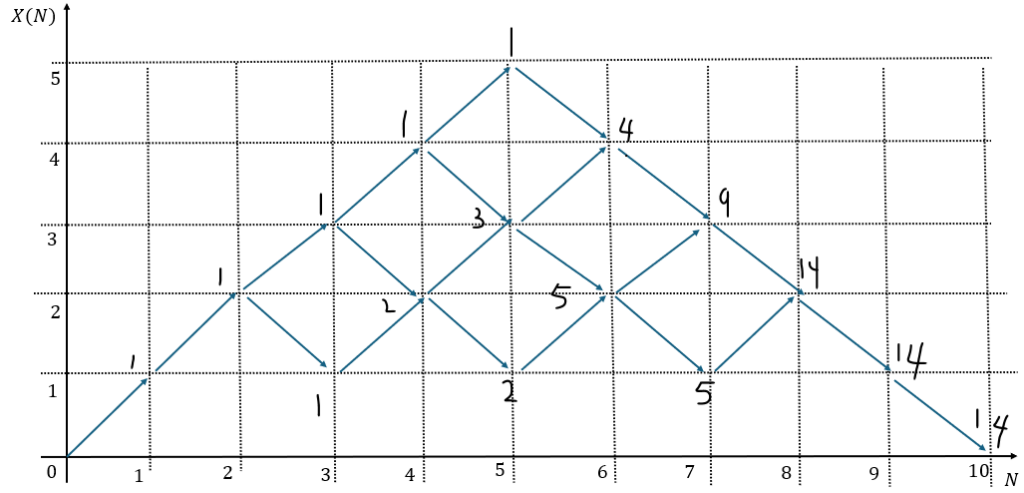
上図を数えると14通りあります。
これと同じ図形がX(N)≦0の領域にもあるので道筋は14×2=28通りです。
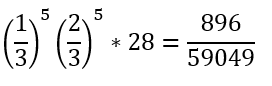
ちなみに、上の道順の数え方は覚えておくと得します。
どういうことかというと(上の図の一部を切り取って解説)・・・
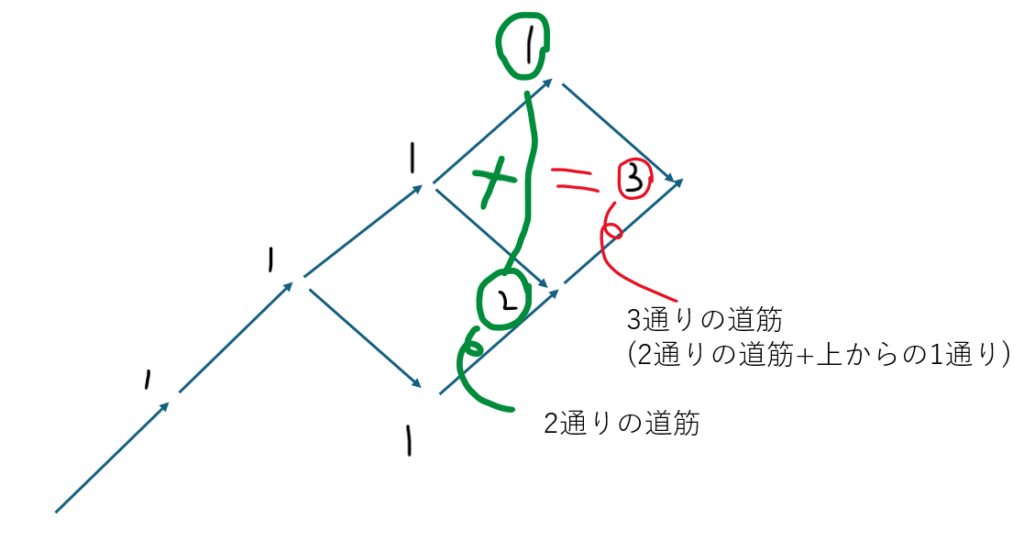



コメント