数直線がループする確率 問題攻略

こんにちは。Horyです。

確率の記事で正多角形がかかわる問題や数直線上を動く点に関する問題に関しては解説したと思います。

今回の記事では数直線がループする場合の確率を攻略します。

今回も頑張りましょう。

数直線のループ問題

以下に示すのは本記事で取り組む問題になります。

この問題を例に解説します。

例えば、正七角形について考えてみましょう。

以下のように数直線で考えてみます。

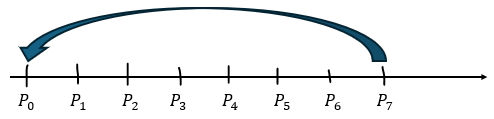
どの問題でも最初にAがいる点をP0として、反時計周りにP1,P2・・・を設定するものとします。

ここで、正七角形ではP0とP7は同じと見なしていいです。

整数分野で学んだmodを効果的に使えそうですねぇ(ニンマリ)。

本問ではmod7で考えてみます。

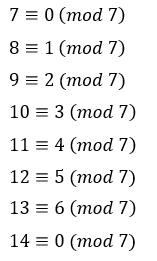
例えば、「反時計回りに8回進むこと」は「反時計回りに１回進むこと」と同じです。

14回サイコロを投げて同じ点に戻ってくる確率はmod 7で計算して合計が0になればいい(7の倍数になる)ですよね。

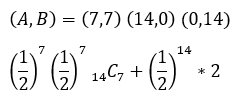
計算は自学自習とします。

本問はmod 8で考えてみます。

計算は自力でやってみてほしいです。

正24角形でサイコロを48回も投げますし、modで考えるのも面倒かもしれませんが、ここまで頑張ってきた皆さんであれば規則性がつかめてきたのではないでしょうか？

というのも、同じ点に戻る確率というのは・・・

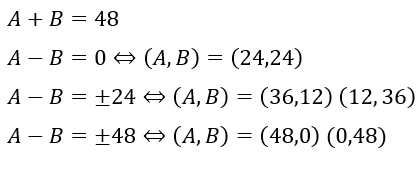
計算は自学自習してください。