こんにちは。Horyです。
今回も面白い問題を紹介します。
皆さんはトランプタワーって知っていますか?
高いトランプタワーを作ることは難しいかもしれませんが完成したときの達成感は計り知れません。
ところで、トランプタワーは無数の三角形が集まってできていますが、あの図形の中に三角形はいくつあるか気になりませんか?
今回はそんな問題に取り組もうと思います。
今回も頑張りましょう。
トランプタワーと三角形の数
以下に示すのは今回の記事で取り組む問題になります。

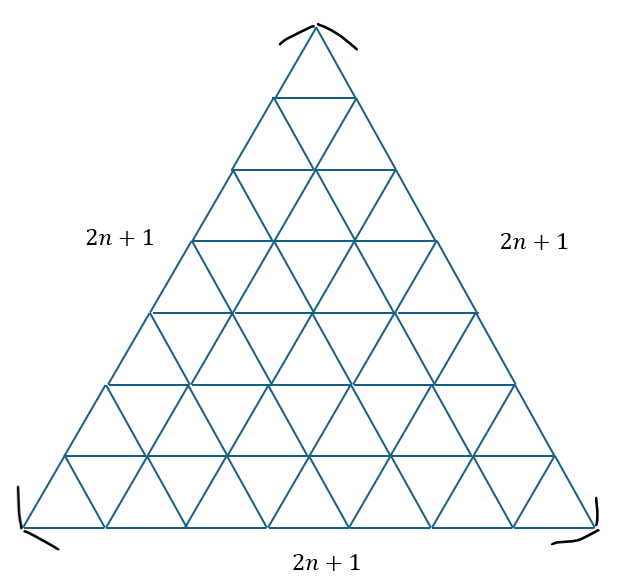
この問題を例に解説します。非常に難しい問題ですが頑張りましょう。
最初に言っておきたいことで、当たり前のことですが、本問題は長さが1の正三角形の総数を求める問題ではありません。
長さが1の正三角形だけでなく、長さが2の正三角形も存在します(長さが1から2n+1の正三角形が存在)。
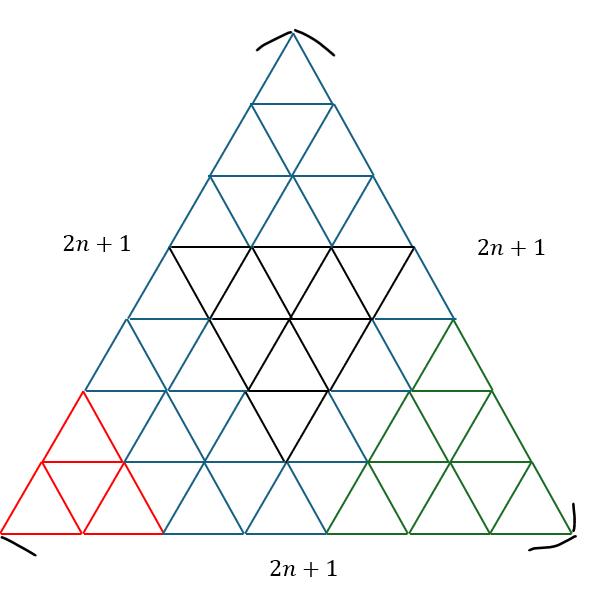
- 赤線・・・1辺の長さが2の上向き正三角形
- 緑線・・・1辺の長さが3の上向き正三角形
- 黒線・・・一辺の長さが3の下向き正三角形
長さだけでなく、向きにも違いがあります。
これらの長さや向き(上下)が異なる正三角形を全てひっくるめるという意味での総数を問うています。
作戦を立てずに正面突破するのは無謀の極みです。戦略は以下の通りです。
- 上向きの正三角形の総数を求める
- 下向きの正三角形の総数を求める
- 上下で足し合わせる
また、一気に正三角形の総数を求めようとしても無理です。
そのため、一辺の長さがkの正三角形の数を求めたのちに、Σを用いて総数を求めます。
上向きの正三角形の総数
まずは、上向きの正三角形の総数を求めます。
一辺がk (1≦k≦2n+1)の正三角形の個数を求めてみます。
何個あるかに関してですが、まずは、トランプタワーそのものの頂点を共有する正三角形(一段目)を考えます。
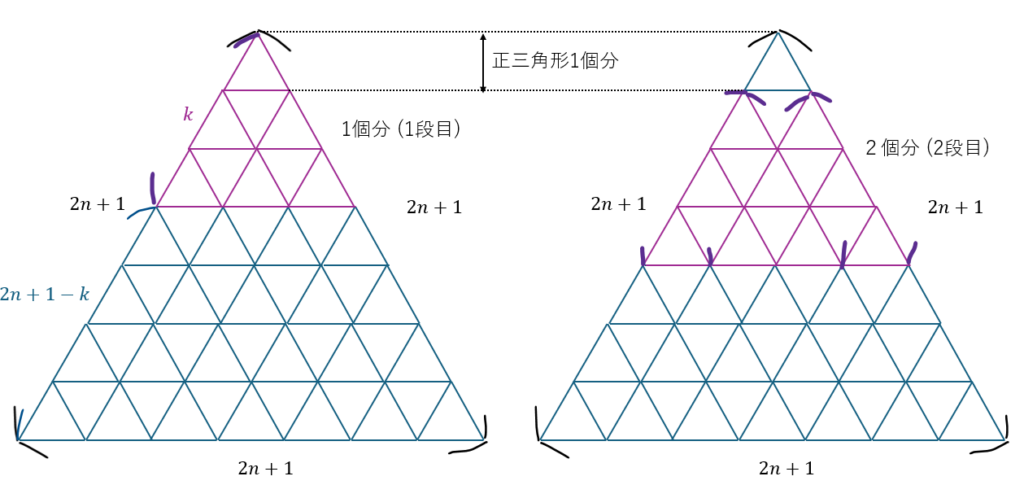
図に関して気づくことをいくつかまとめます。
- 1段ずつ下げて正三角形を作ることができる
- 1段下げると三角形の数は1個増える
- 最下層は「(2n+1)-k+1」段目に「(2n+1)-k+1」個の正三角形
長さがkの上向き正三角形の数は以下のように記述することが可能です。
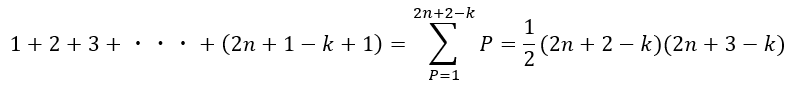
上の和のkをk=1からk=2n+1まで足し合わせます。
愚直に計算してもできます。ただ、ちょっと大変なので工夫します。
どういうことかというと、これって式が複雑になっていますが、連続する自然数の積ですよね!
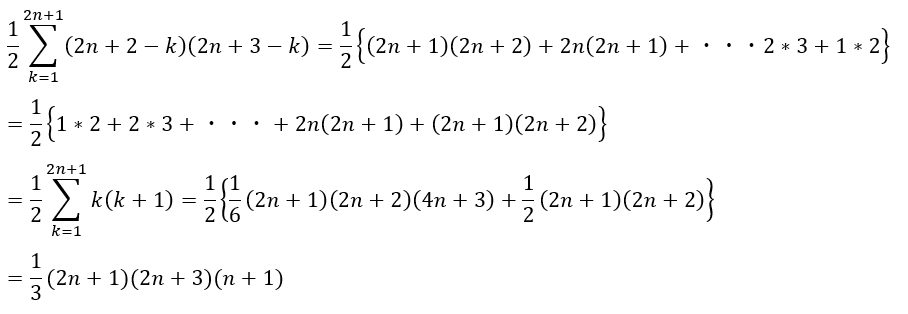
下向きの正三角形の総数
下向きの正三角形は上向きとは考え方がかなり違うので注意が必要です。
一辺がk (1≦k≦n)の正三角形の個数を求めてみます。
上向きの正三角形の一段目と対をなす状態を下向きの正三角形の一段目とします。
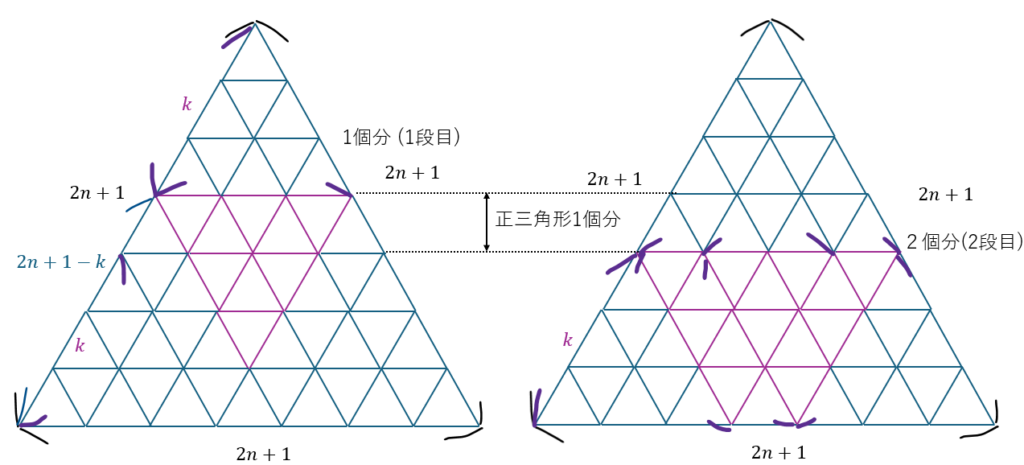
図に関して気づくことをいくつかまとめます。
- 1段ずつ下げて正三角形を作ることができる
- 1段下げると三角形の数は1個増える
- 最下層は「(2n+1)-2k+1」段目に「(2n+1)-2k+1」個の正三角形
ところで、正三角形の最大辺の長さがnの理由ですが、最下層の正三角形の数(1以上)に関係します。
(2n+1)-2k+1 >0 ⇔ k < n+1 ⇔ 1≦k≦n
以上が理由になります。
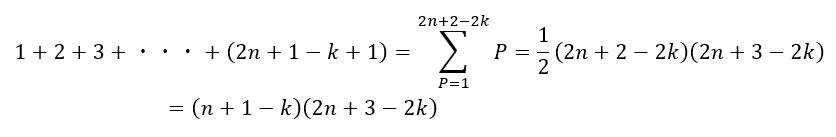
上の和のkをk=1からk=nまで足し合わせます。
愚直に計算してもできます。ただ、ちょっと大変なので工夫します。
どういうことかというと、これも元を辿れば連続する自然数の積です。
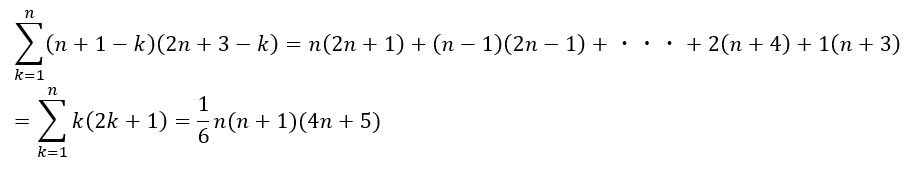
正三角形の総数
先ほど導出した上向きの正三角形と下向きの正三角形の総数を足せばいいだけです。
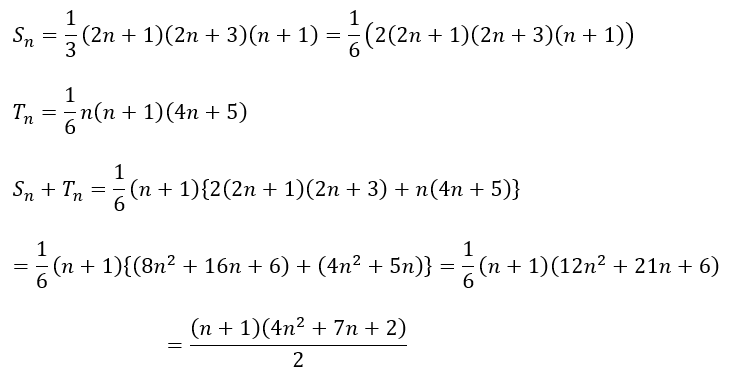
以上により総数を求めれました。



コメント