こんにちは。Horyです。
正多角形で場合の数や確率の問題を作ると基本的な問題から応用問題まで幅広く作れます。
今回の記事では正多角形をテーマにした場合の数・確率の問題に取り組みます。
今回も頑張りましょう。
正多角形と場合の数
正多角形と場合の数が関係する問題になります。

この問題を例に解説します。
図形に関する確率や場合の数についてのポイントを以下にまとめます。
- 図形の場合の数・確率のポイント
- 点の固定
- 辺の固定
- 面の固定
- 長さの固定
空間図形の場合は切って断面で見ることや、展開して二次元にすることも効果的な場合があります。
また、場合の数であることに注意です。「同じモノ」は区別しません(大原則)。
(1)解答・解説
(1)の解答・解説になります。
これは比較的に簡単な問題なので答えられると良いです。
どちらの場合も頂点を任意に二つ選ぶ場合の数から辺の数を引けば良いだけです。
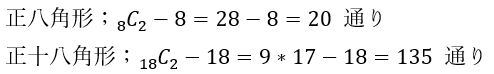
(2)解答・解説
この問題が非常に難しい問題になります。
Aは固定されているとして、点Aは頂点だが、Aを含む辺を共有しなければいいので頂点がAを含んだ辺からどれだけ離れているかを考えればいいです。
正多角形は対称的なので時計回りor反時計回りは議論しなくてもいいです。
x,y,zを1以上の整数とします。
- 点Aから辺をx本通り過ぎたところは2番目の頂点
- 2番目の頂点からy本通り過ぎたところは3番目の頂点
- 3番目の頂点からz本通り過ぎたところは点A

以下は答えの二通りの図形です。「x=2」の場合です。
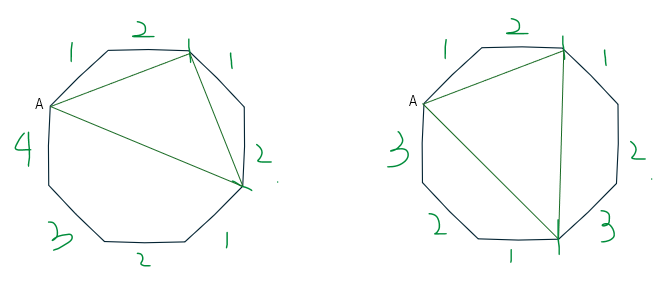
一方で以下は「x=3」の場合ですが、これは回転させると「x=2」の場合と同じになります。
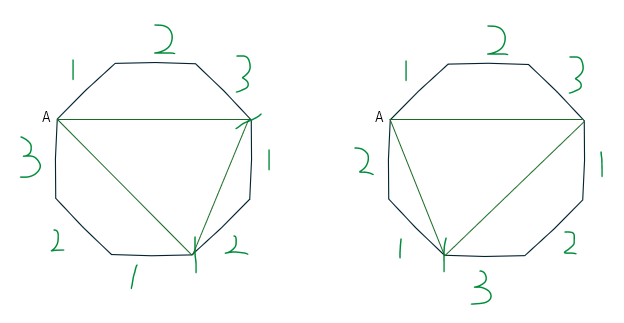
場合の数では同じものを区別しないので二通りしかありません。
正十八角形の場合は自分の力でやってみてください。
正八角形と同様の方法を用います。
正多角形と確率

この問題を例に解説しようと思います。
本問は確率に関する問題です。
確率では同じモノであっても区別します(大原則)。
なので、回転して同じ図形になったとしても点の位置が異なるのであれば違うものとして扱います。

事象の量が多い時は予め文字で置いて簡略化するのが有効です。
また、サイコロから確率を考えるので・・・
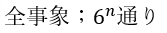
(1)解答・解説
解答・解説になります。

- 赤い部分・・・1点だけが選ばれる
- 青い部分・・・2点だけが選ばれる
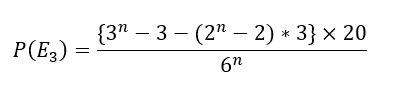
(2)解答・解説
- 2辺を共有・・・三角形;6通り (三角形なら隣り合う2辺)
- 1辺を共有・・・三角形;6×2 = 12通り (2辺を共有しない)
何で12通りか分からない人は実際に図形を書いて考えてみてほしいです。
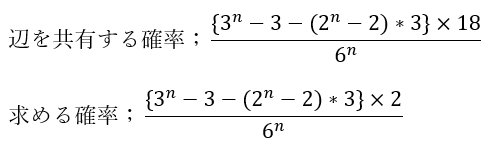
(3)解答・解説
まぁ、やってみればわかると思いますが、対角線があるときに必ず直角三角形ができます。
直接的に求めるのは面倒なので余事象を用います。




コメント