こんにちは。Horyです。
今回の記事では「累乗-1」と倍数に関する問題に取り組みます。
このような問題は難易度としては非常に簡単かもしれませんが、攻略法がたくさんあって非常に面白いです。
1つの解放だけではなく様々な視点から問題を攻略することも数学の醍醐味であると思います。
今回も頑張りましょう。
今回の問題
以下に示すのは今回の記事で取り組む問題です。

この問題ですが、思いつくだけでも解答方法が6つぐらいあります(全部思いついたらたいしたもんです)。
- 数学的帰納法
- 二項定理
- 合同式 (mod)
- 等比数列
- 漸化式
- N進数
これらの解答方法に関して個別に解説していきます。
頑張りましょう。
数学的帰納法
数学的帰納法に関する記事はこちらにまとめています。

以上からn=k+1の時も4の倍数であることが示せたので帰納的に4の倍数であることが示せました。
この問題をたくさんの学生に出してきましたが、一番思いつく方法かと思います。
二項定理
二項定理による方法です。記事は以下に示すとおりです。
5が1と4の和であることを利用する方法です。
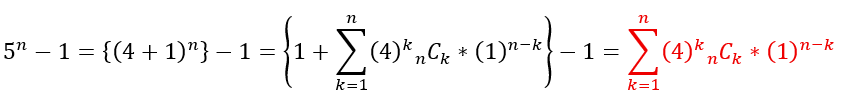
結局、Σは4の倍数になるので4の倍数です。
合同式 (mod)
合同式を用いる方法です。記事は以下に示すとおりです。
これも5が1と4の和であることを利用しています。
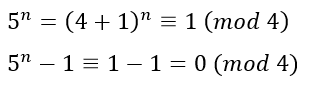
以上から4の倍数になります。
等比数列
等比数列を用いる方法です。記事はこちらです。
この数列は初項が1で公比が5の等比数列と言えます。
この等比数列の和を考えます。
初項と公比から和が自然数であることは明らかです。
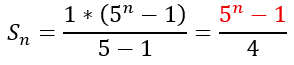
赤い部分は題意の式ですが、和が自然数になるためには分子が分母の4で割り切れないといけません。
以上から題意の式は必ず4の倍数になります。
漸化式
漸化式を用いる方法になります。記事はこちらです。
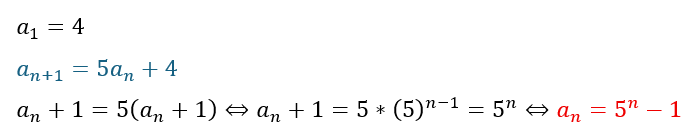
上の式の赤い部分は題意の式になります。
初項が4であることと、青い部分(漸化式)より、前の項の5倍に4を足しているので4の倍数であることは自明です。
N進数
N進数を用います。記事はこちらです。
ここからは、5進数で表します。

赤い部分は0がn-1個存在します。
ここで、P=5として計算をPで表します。
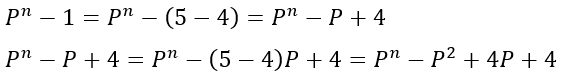
皆さん、お気づきかもしれませんが、これを繰り返してマイナスを除去していくと最終的に「Pのn乗」が消えることになります。
最終的には、、、
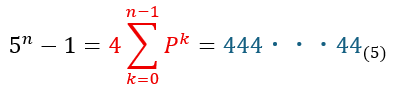
赤い部分が4の倍数になるので4の倍数です。
青い部分は5進数で4がn-1個並んでいます。



コメント