こんにちは。Horyです。
今回の記事では指数や階乗を用いて表される数の中に素因数がいくつ入っているかというテーマの問題に取り組みます。
特に階乗中の素因数の数については公式があってルジャンドルの公式と呼ばれています。
今回も頑張りましょう。
ルジャンドルの公式 問題
以下に示すのはこの記事で取り組む問題になります。

この問題を例に解説します。
このままやっても難しいので簡単な数で実験をしてみましょう。
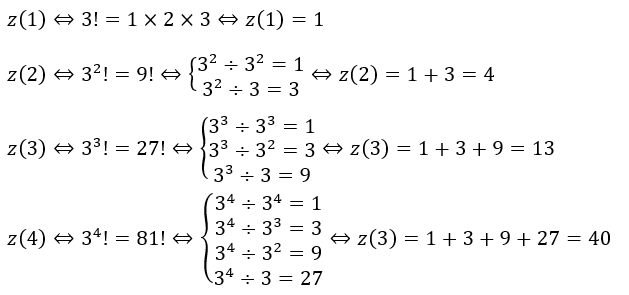
上のことを考えると、N!の中の素因数(P)の数はガウス記号を用いて以下のように表せます。
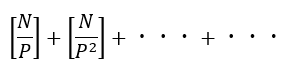
ここで、3^5を用いて上の方法と異なるやり方で導出してみます。
243までの自然数のうち、(3^k)×(≠3の倍数)の数をakとします。
ただし、kは1~5までの自然数とします。
もっとわかりやすく解説すると、、、今回は243!なので焦点にする数は243です。
- 243の中に3の数は81個
- その中で(3^k)×(≠3の倍数のモノ)は・・・
- 81から3×(3の倍数)の数を引いたもの
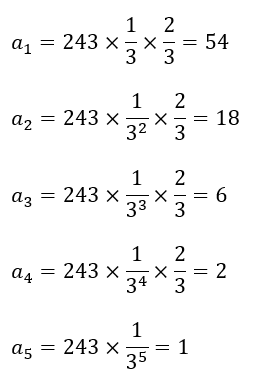
1~4において(2/3)倍しているのは(3^k)×(3の倍数)の数を引いていると思ってください。
これを用いて243!の中に3が何個あるのかを考えると・・・
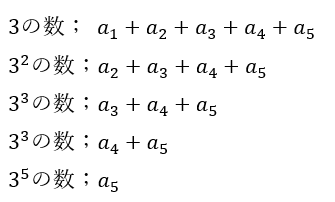
素因数3の数は上の全ての和なので・・・
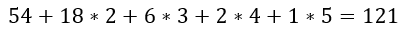
この方法を応用していきます。
解答・解説
問題の解答・解説になります。
今回は3の数なので3の倍数であることに注意してください。
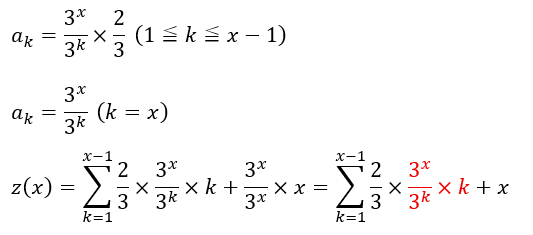
ここで、上の式の赤い部分を考えます。
これは等比×等差 による和の公式になります。
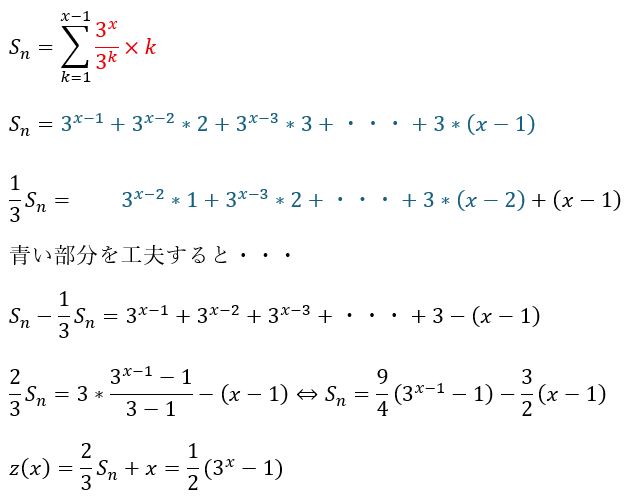
ここで解答を終わってはいけません。
Σの上の数が「x-1」で下の数は「k=1」になっています。
これはΣの意味から「x=1」を代入できないことを意味しています。
そのため、「x=1」は別で代入して調べないといけません。
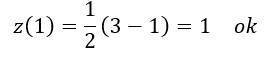
以上が解答になります。


コメント