こんにちは。Horyです。
今回の記事でも整数問題に取り組もうと思います。
今回の問題は「tan 1°」が有理数であるかどうかに関する問題の解説を行います。
非常に有名な問題なので解説するまでもないと思いますが、意外な落とし穴もありますので、その辺の理由も含めて詳細に解説します。
今回も頑張りましょう。
「tan 1°は有理数か」
問題の攻略に移ります。
まず、直接的な証明は難しそうなので背理法を用います。
背理法に関する記事はこちらです。
tan 1°は有理数ではなさそうなので無理数ということを証明したいですが、このままでは無理そうなので有理数と仮定して矛盾を導くという方針で進めたいと思います。
矛盾の導き方
まずは、「tan 1°が有理数である」と仮定します。
ただ、tan 1°だけではどうすることもできなさそうなので数を増やします。
加法定理が使えそうですね。
加法定理に関する記事は以下に示すとおりです。
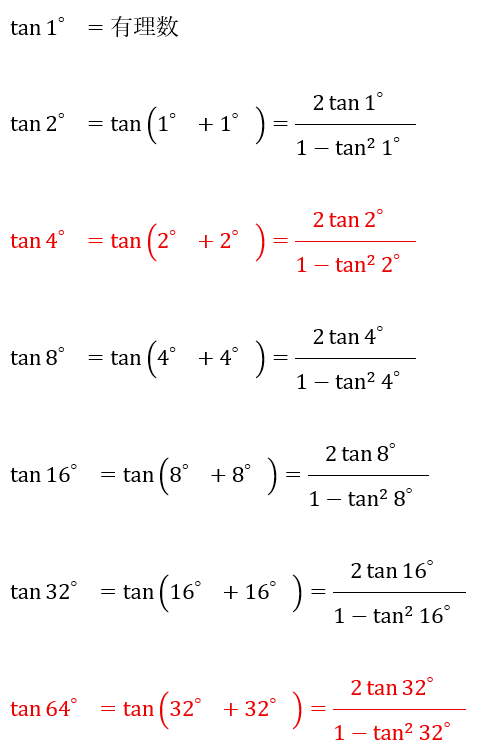
ここで、tan 1°を有理数として加法定理でtan 2°を導出しましたが、tan 2°は有理数の比で表されます。
そのため、tan 2°は有理数になります。
以上から4° 8° 16° 32° 64°も連鎖的に有理数になります。
ところで、「64°- 4°= 60°」ですよね。
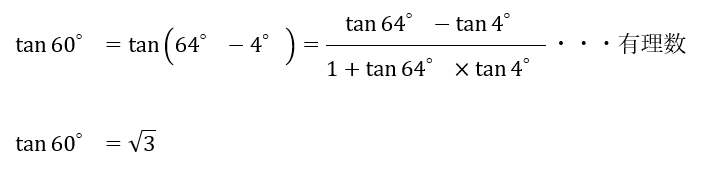
以上からtan 1°を有理数と仮定して議論を進めると加法定理でtan 60°も有理数の比になって有理数になるが、tan 60°は√3で無理数なので等号関係に矛盾が生じる
以上のことからtan 1°は無理数である。
として解答を終わらせると減点になります。
一見して隙のないような解答になりますが、減点されます。
減点される理由
上の解答がどうして減点されるのかというと、、、
そもそも、この問題は「無理数であることを証明する問題」です。
tan 60°が√3であることは誰でも知っていると思いますが、「無理数であることを示す問題」で√3が無理数であることを証明することなく決めつけてしまっても良いのでしょうか?
この問題の最大の落とし穴で√3が無理数であることを証明しなければなりません。
これも背理法で示します。

ここまでやって√3が無理数であると分かったので、等号関係に矛盾が生じるからtan 1°は無理数である。
これで満点の解答です。
背理法の二段構えの非常に良い問題です。



コメント