こんにちは。Horyです。
今回も前回に引き続き整数問題に取り組みます。
今回取り組むのは多項式が関係する整数問題の攻略です。
今回も頑張りましょう。
問題
以下は本記事で取り組む問題です。
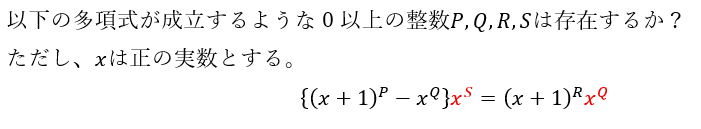
この問題を例に解説します。頑張りましょう。
問題を解く前の下準備
まずは、問題を解く前の下準備です。
整数問題の定石は掛け算の形で問題の式は積の形になっているから(約数)×(約数)で解決できるか・・・と思うかもしれませんが無理です。
何故なら、今回は自然数がP,Q,R,Sでxは実数です。
そのため、xが整数ではない場合が普通にあります。
どうしたものかと思いますが、こんな時に使える方法こそ簡単な数値や極端な数値の代入による実験です。
どういうことかというと、P,Q,R,Sが特定の数なら、xが(正の実数なら)どんな値でも成立するということです。
どんなxでも成立するなら都合のいい数を代入しても成立します。
「x=1」を代入するのはどうでしょうか?
上の式の赤い部分が1になって式が簡単になりますよね。。。
このような方法を数値代入法といいます(覚えといてください)。
また、以下のことも重要です。
- 「有理式の等式」は「多項式の積の等式」
- 「有理式の等式」は「多項式の比の等式」
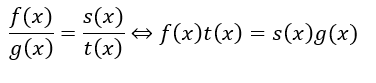
数値代入法 ①
数値代入法によりx=1を代入します。
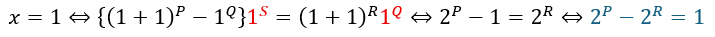
ここで、当たり前のことですが重要なことです。
- 偶数±偶数 =偶数
- 奇数±奇数 =偶数
- 偶数±奇数 =奇数
上のことは素数の和や差が素数になるような問題で非常に役に立ちます(偶数の素数は2だけ)。
本問では青い式の左辺が1(奇数)になっていて右辺はPとRがどちらも0より大きければ「偶数-偶数」で偶数になります(P>R)。
そのため、「R=0」「P=1」になるしか左辺が奇数になる道は残されていません。
数値代入法 ②
先ほど求めたPとRを代入してみます。

ここで、定石である積の形が使えます。
というのも、右辺の値はxが0以上の実数であることから必ず正になります。
右辺が正になるためには左辺も正にならないといけないです。
そのためには、式の緑の部分が正にならないといけないです。
ひとまず、このままではだめなので、「x=2」を代入してみましょう。
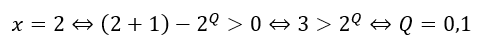
Qの値を絞り込めました(ニンマリ)。
P,Q,R,Sの特定 (落とし穴に注意)
とりあえず、P,Rは求めれて、Qは二通りに絞り込めたので代入してみます。

以上により「P=1」「Q=1」「R=0」「S=1」で求めれました。「やったぜ!」で解答を終わらせてしまう人がいます。
実にもったいなく残念なことです。
何でこのままではだめなのかというと、P,Q,Rの求め方にあります。
- P,Rの求め方・・・「x=1」を代入して求めた
- Qの求め方・・・「x=2」を代入して求めた
上のように求めたかもしれませんが、そもそも、題意の等式は全ての正の実数で成立します。
なので、xの候補なんて無限にあります。
無限個の候補の中の一つを代入して成立したからと言って確認もせずに全ての候補で成立すると言ってしまっていいのでしょうか?
このようなことを数学では「十分性の確認」や「十分条件の確認」といって、この確認を怠ると解答が「必要条件しか示していない」という理由で確実に減点されます。
多項式の数値代入法は十分性の確認が落とし穴になります。
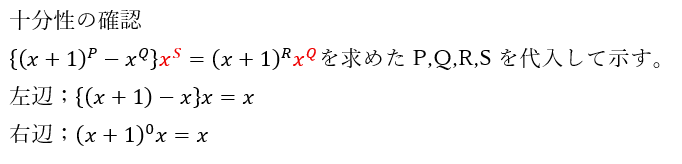
以上から右辺と左辺が等しくなるので、確かに全ての場合で成立します。
以上で満点の解答になります。
みんなも「十分性の確認」には気を付けよう!



コメント