こんにちは。horyです。
今回の記事では連続する自然数と互いに素に関する問題の攻略記事を書こうと思います。
今回も頑張りましょう。
問題
以下に示すのは今回の記事で取り組む問題になります。

この問題を例に解説します。
問題を解く前の下準備

- 10000は素因数に2と5を持つ
- 連続する2つの自然数の積 「整数問題の定石_(約数)×(約数)」
ところで、連続する自然数は必ず偶数と奇数になります。
偶数と奇数なので互いに素(1以外に公約数を持たない)だと思いますが、「偶数と奇数だから互いに素」として議論を進めるのは論理の飛躍です。
本当にそうなっているか確かめる必要があります。
(連続する2つの自然数が互いに素というのは覚えておいた方がいいです)
連続する2つの自然数が互いに素の証明
連続する2つの自然数が互いに素ということを証明します。
背理法を用いますが、実は、以下の記事ですでにやっています。
ただし、復習のために本記事でも一からやります。
背理法の矛盾の導き方は「前提と矛盾する」「等号に矛盾する」のどちらかです。
今回の場合は「前提と矛盾する」ことを導き出します。

以上が証明になります。
何気ないことかもしれませんが、これがこの問題の突破口になります。
互いに素と倍数 (範囲の絞り込み)
連続する2つの自然数は互いに素です。
ということは、xとx-1は1以外に公約数を持ちませせん。
10000の素因数は2と5しかありません。
これが意味することは、xとx-1を素因数分解したときに2と5が混在してはいけないことを意味します。
今回はxが奇数と問題文にあるので、xは約数として必ず5^4=625を持ちます。
また、xの素因数に偶数が混在してはいけないので9999以下のxは以下のように絞り込めます。
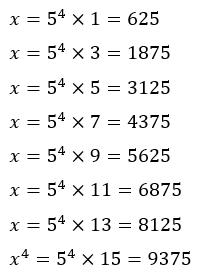
こんなところでしょうか?
候補を8個に絞り込めました。
絞り込み→特定
絞り込みは行ったので特定を実施します。
一番スマートなやり方はmodを使う方法です。
2^4=16なので、mod 16を考えると・・・
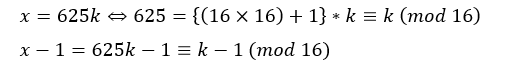
以上から、本問ではx-1が16の倍数になるときはk=1の時なので、そのような奇数xは625のみです。
もう一つ方法があります。地道に計算を行う方法です。
こういった泥臭いやり方を嫌う人が結構いますが、数学で泥臭い計算をするのは日常茶飯事(特に数Ⅲ)です。
泥臭く計算をする方法も知っていいてほしいです。
また、泥臭い方法でも工夫すれば楽になります。
例えば、倍数の判定法に関する記事でも解説しましたが・・・
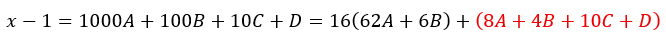
もちろん、A,B,C,Dは0以上、9以下です。
赤い部分が16になれば必ず16の倍数になるので、素因数分解するよりも楽かもしれません。
また展開公式より、、、
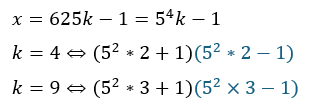
青い部分は偶数になりますが素因数2を4個も持たないので絶対に16の倍数にはなりません。このことから、4,9は即座に除外できます。
こういった愚直な計算を工夫できる人とそうでない人では数学力に雲泥の差がつきます。


