こんにちは。Horyです。
前回の記事ではN進数の基本事項に関してまとめると共に、小数をN進法でどのように表すかについてまとめました。
今回の記事はN進数の四則演算で「足し算・引き算・掛け算・割り算」に関してまとめようと思います。
今回も頑張りましょう。
N進数の四則演算
N進数の四則演算について、高校の教科書や市販の参考書では筆算による計算方法が書かれていると思いますが、正直、やりにくいし、ミスが生まれやすい方法であると思います。
しかも、本末転倒になってしまうかもですが、N進数の状態で計算しなくても、十進数で四則演算を行った上で、計算結果をN進数に直せば済む話です。
ただ、それだと、この記事の意味がなくなってしまうので、今回は、N進数のまま計算を行える方法を紹介したいと思います。
以下は今回取り組むN進数の四則演算の問題になります。

ひとまず、10進法に書き直してみます。
- 10112(3)・・・95
- 2022(3)・・・62
- 111212(3)・・・374
- 122(3)・・・17
- 和;95+62=157
- 差;95-62=33
- 積;95*62=5890
- 商;104÷17=22
このような問題が出たときに筆算でやろうとするとミスが生まれやすくなります。
そのため、P=Nとして数を以下のように表すと効果的です。
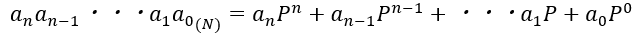
今回の問題は3進数だから、P=3です。
足し算
題意の数をPで表してみます。
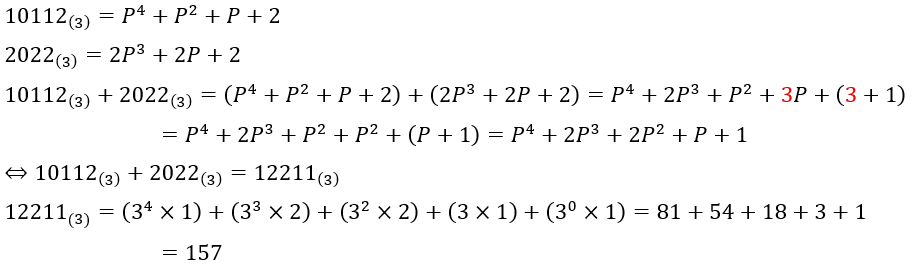
10進法で計算した結果と一致しました。
引き算
題意の数をPで表します。
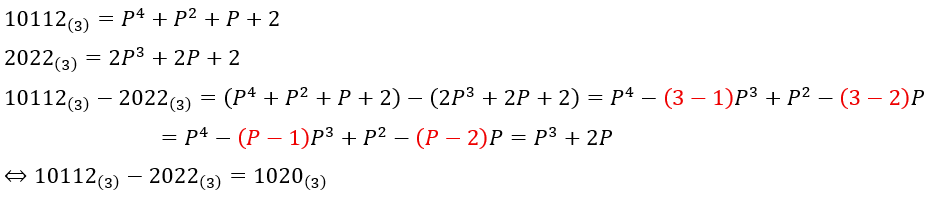
上の式の赤い部分がポイントで、Pに直したときにマイナスを登場させたくないので、マイナスになる次数の係数は3から引いた値で対応させています。
これを行うことで、導出される式にマイナスが登場しなくなります。
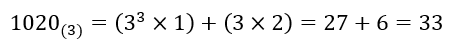
10進法で計算した結果と一致しました。
掛け算
題意の数をPで表します。

計算は大変かもですが、十進法での計算結果と一致します。
割り算
題意の数をPで表します。
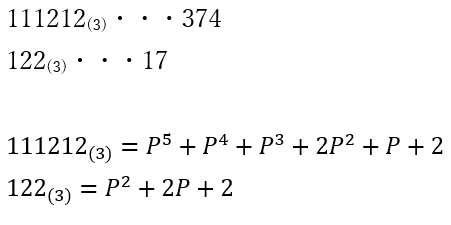
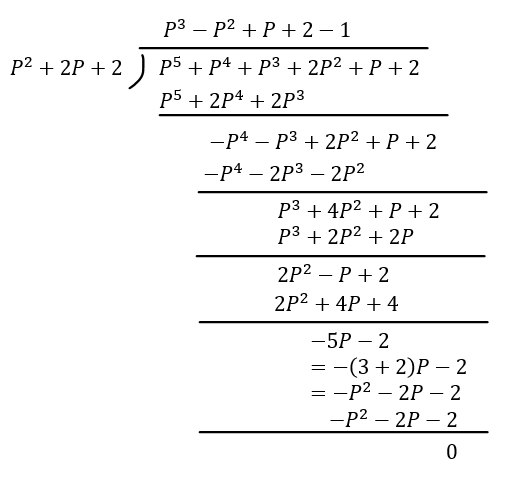
よって商は以下のように表せます。

実際の割り算と計算結果が一致します。



コメント