こんにちは。Horyです。
前回の記事では「データの分析」最初の記事として高校数学におけるデータの分析の位置づけや考え方やヒストグラムの作り方を解説しました。
上の記事は必ず読んでおいてください。今後の数Ⅰの「データの分析」や数Bの「確率分布関数」も上の記事の考え方をベースとして話が進んでいきます。
今回の記事では代表値に関して説明しようと思います。
高校数学で学習する代表値の定義を理解すると共にメリットとデメリットを説明します。
今回も頑張りましょう。
代表値について
代表値とはデータの特性を定量的に表した数値のことです。
高校数学で学習する代表値は主に以下の3つになります。
- 平均値
- 中央値
- 最頻値
これらについて定義を解説すると共にメリットとデメリットを紹介します。
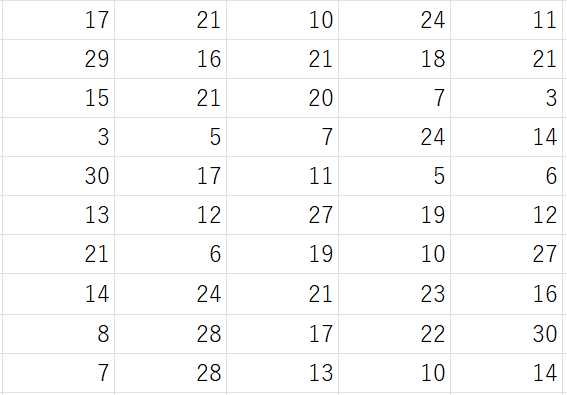
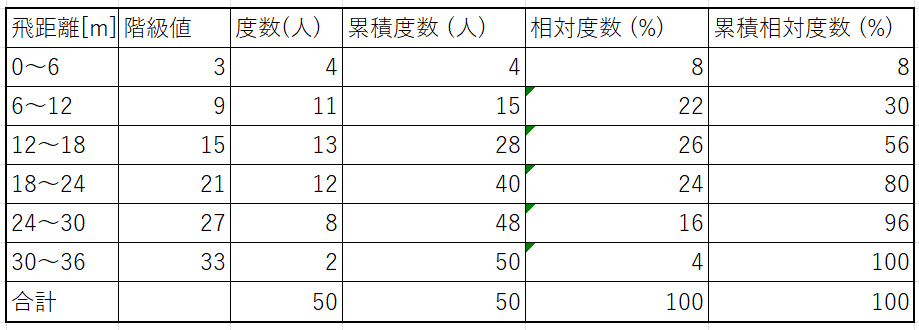
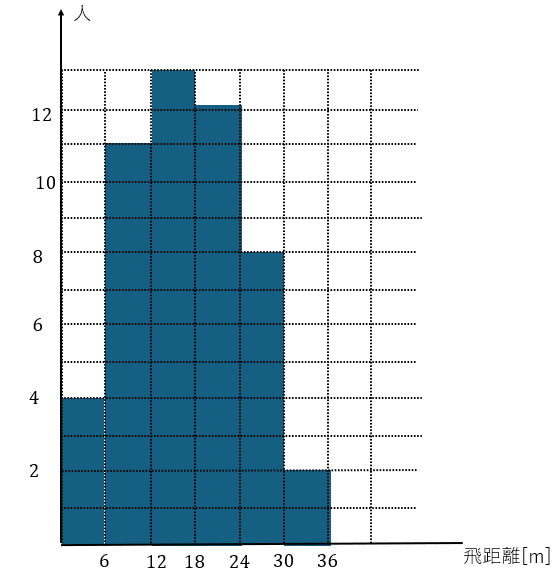
また、用いるデータに関しては前回の記事で用いたボール投げの飛距離を用います。
平均値
最初に平均値についてです。アベレージ(average)とも言います。
私たちが日常で生活する中で最もなじみ深い統計量だと思います。
n個データ(X1,X2,X3・・・Xn)があると考えると平均値は以下のように立式できます。
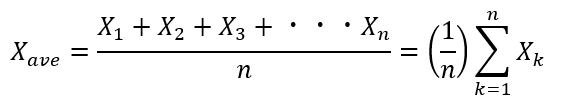
Σ記号に関しては以下の記事に書かれていますので読んでおいてください。
簡単に説明すると、平均値とは「全データの数値の和」を「データの数」で割った値です。
前回用いた50個のデータであれば・・・
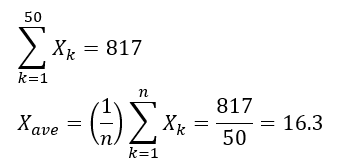
ちなみに、平均値は変量(我々は生データと呼んでいる)の桁数よりも一桁多く記述するのがルールになります。
今回はボール投げの飛距離は整数なので、平均値は小数第一位まで記述します(今回なら小数第二位を四捨五入した)。
共通テストで代表値を計算で求める問題も出るかもしれないので覚えておきましょう(まぁ、大抵はきれいな数字になって、迷うことはあまりないと思いますが・・・)。
- 平均値のメリット・デメリット
- メリット・・・データ全体の特徴を定量的に説明可能 (データ数が膨大でも大丈夫)
- デメリット・・・外れ値の影響を大きく受ける
デメリットの「外れ値の影響を大きく受ける」とはどういうことかと言うと、、、
明らかに異常なデータであっても定義上、計算に含めてしまうので、外れ値がある状態で平均値を求めると誤った推測を導いてしまう可能性があると言うことです。
そのため、平均値を考えるときには予め外れ値 (著しく外れた値)を除外して考える必要があると言うことです。
外れ値について気になる人は「レジェンド校長 横浜」とgoogleで検索してみてください。
もし、それを統計データの中に組み込んでしまった場合、日本の教育界は大変なことになるでしょう。だから、外れ値は除外して考えないといけないのです。
平均値の罠
平均値の罠について解説します(これも共通テストで良く出ると思います)。
以下に示すことは正しいでしょうか?
(ただし、A,Bの両クラスとも同じテストを受けて点数をクラスごとに記録したとする)
- Aクラス
- 学生・・・50人
- 男子の平均点66点
- 女子の平均点74点
- Bクラス
- 学生・・・50人
- 男子の平均点67点
- 女子の平均点88点
問題;「男子も女子も平均点はBクラスの方が高いので、クラス全体のテストの平均点もBクラスの方が高い」・・・○か×か?
ここで、○と答えてしまった人は罠に引っかかっています。
「何でやーー?」と思うかもしれませんが極端な例を考えてください。
もし、「Aクラスは男子も女子も25人」で、「Bクラスは男子が48人、女子が2人」のような場合ならどうでしょうか?
男子と女子の内訳が分かっていない段階で決めつけてしまうのは危険です。
ちょっと計算してみます。
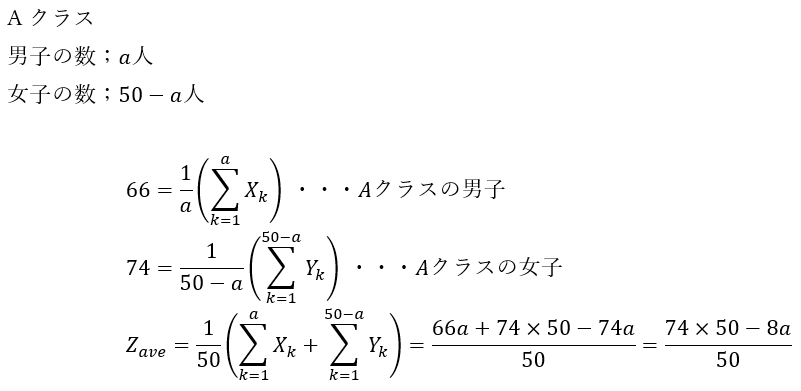
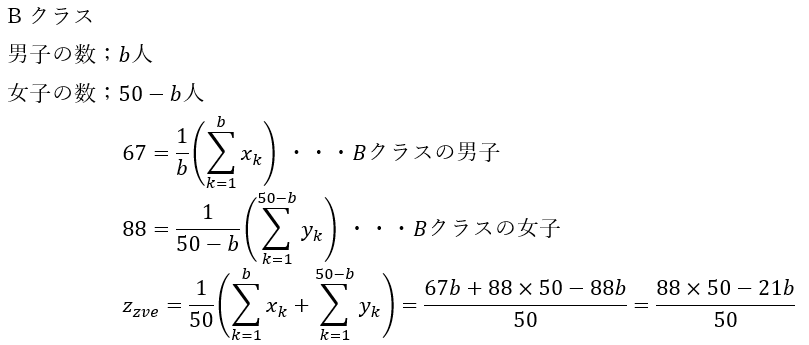
仮にa=25, b=48を代入して全体平均を求めると・・・
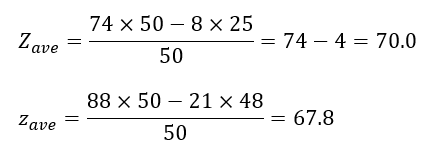
上の値を比較するとクラスAの平均点の方が高くなっています。
そのため、問題の答えは×です(Aクラスの方が高くなるときが状況的にあり得るから)。
平均値の罠;その2
以下の場合であればどんな状況でもBクラスの得点の方が必ず高くなります。
- Aクラス
- 学生・・・50人
- 男子の平均点66点
- 女子の平均点74点
- Bクラス
- 学生・・・50人
- 男子の平均点80点
- 女子の平均点88点

- 最小の場合・・・Bクラスの男子が50人でAクラスの男子が0人
- 最大の場合・・・AクラスとBクラスで男子の人数が等しい
よって、この場合は男女の内訳に関係なくBクラスの方が必ず得点が高くなります。
中央値
中央値とはデータを小さい方から順に並べたときに中央に来る値のことです。
メジアンとも呼ばれています。
気をつけなければならないことはデータ数が奇数個の時と偶数個のときで処理が違うことです。
- データ数が奇数;1,2,3,4,5・・・中央値 = 3
- データ数が偶数;1,2,3,4,5,6・・・(3+4)/2 = 3.5
データ数が偶数の時は、中央の2つの和を2で割った値が中央値です。
- 桁数について
- 個数が奇数;中央値は元のデータの桁数に合わせろ
- 個数が偶数;中央値は元のデータの桁数より一桁多くしろ
- 中央値のメリット
- データ数が少なくても機能する
- 外れ値の影響を受けにくい
- データの偏りを定量的に評価 (外れ値の影響を受けないことの言い換え)
- 中央値のデメリット
- データ全体を定量的に評価できない (部分的に見てる)
最頻値
最頻値はデータをどういった観点で見るかで値が異なってきます。
- 生データで見る・・・データの中で最も多く出てくる変量
- 度数分布表で見る・・・最も度数の大きいデータの階級値
上のボール投げの例で最頻値を考えると・・・
- 生データ・・・21 [m] (6個あった)
- 度数分布表・・・「12~18」(階級値なので15)
最頻値はモードとも呼ばれています
- 最頻値のメリット
- データ数が少なくても機能する
- 外れ値の影響を受けにくい
- どれが一番多いかが一発で分かる
- 最頻値のデメリット
- データ全体を定量的に評価できない (部分的に見てる)
- 生データだと1つに定まらない可能性がある
- 度数分布表だと区間幅を変えると最頻値が変わる


コメント