こんにちは。Horyです。
電磁気学の理論を応用した装置にサイクロトロンという装置があります。
今回の記事ではサイクロトロンについて簡単に解説します。
今回も頑張りましょう。
サイクロトロン
サイクロトロンとは以下に示す装置のことです。
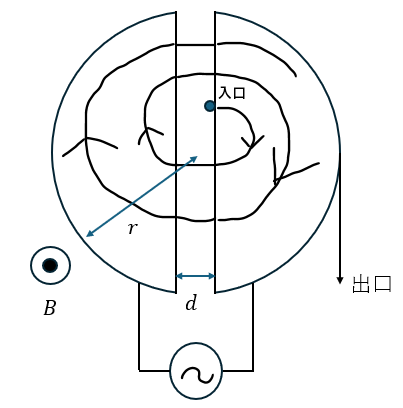
サイクロトロンとは上図のように二つの半円形の電極を交流装置につないだ装置になります。
そもそも、何でこんな装置ができたのかというと・・・
- 量子力学の台頭→ミクロな世界の原理を知りたい
- 原子核反応を起こしたい
- 原子を壊して構造を調べたい
- 課題;クーロン斥力に逆らって核を接触させるのに巨大なエネルギー
- 解決策;原子核を加速させればいい
原子核は陽子が正の電荷を持つので接触させるには斥力に逆らうぐらいに加速させないと無理です。
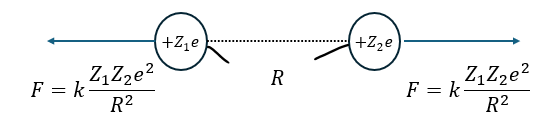
つまり、サイクロトロンとはイオンなどの荷電粒子加速装置です。
交流により半円の電荷の正負を周期的に変えることで、荷電粒子が電源からエネルギーをもらい、グルグルしながら加速します。
加速するタイミングは半円から半円に移るときです。
半周するまでの時間
半周するのにかかる時間を考えます。
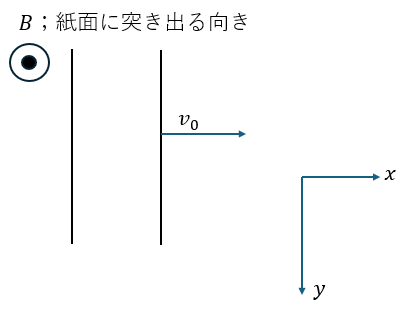
上図を参考にします。磁場あるところにローレンツ力ありなので向きを計算します。
荷電粒子(電気量q)の出発地点を起点に考えると・・・
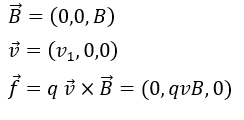
よって、ローレンツ力は円の中心に向かって働くと考えていいです(他の地点でも速度の向きをよく考えて磁場との外積を考えると納得できると思います)。
円運動の運動方程式に当てはめます。
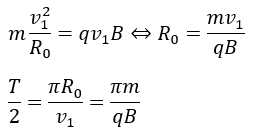
半周する時間を求めれました。ここで、重要なのは半周する時間は荷電粒子の速さによらないということです。
荷電粒子の質量・電気量と印可磁場は定数なので、半周する時間も定数です。
エネルギー保存則
半円間に生じる電位差が常にV0と考えます。
以下のような条件でエネルギー保存則を考えます。
- 最初に半円間を移動 (右から左へ)
- 右半円・・・正
- 左半円・・・負
- 左半円に対して右半円の電位はV0
- (右半円から出る直前)と(左半円に入った瞬間)のエネルギー保存則
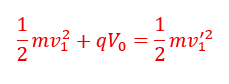
- 次に半円間を移動 (左から右へ)
- 右半円・・・負
- 左半円・・・正
- 右半円に対して左半円の電位はV0(交流で向き変えた)
- (左半円から出る直前)と(右半円に入った瞬間)のエネルギー保存則
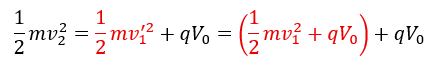
ここで、気づく重要なことは一周するごとに荷電粒子がもらうエネルギーは2qV0だけ増加しています。
脱出するときの状況
荷電粒子がこの円盤を脱出するときは・・・
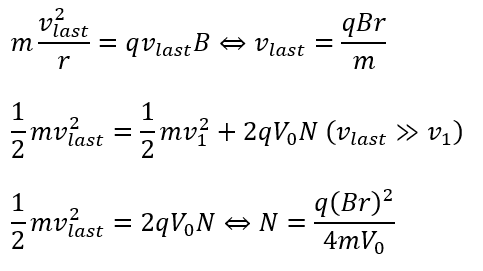
脱出するときの速度は最初の速度とは比較にならないぐらい速くなってないと原子核は壊せません。
そのため、上の式で最初の運動エネルギーは無視します。
脱出するまでの回転数を求めることができました。
まとめ
最後にまとめです。
このような装置でイオンを加速するのですが、効率よく加速するためにはどうすればよいでしょうか・・・?
ここで、重要なのが半周するまでにかかる時間はイオンの速度によらないという点です。
つまり、半周するまでの間に交流電源の位相が(2n-1)πずれるように設計すれば効率よく加速できますね(半周する段階でちょうど左と右半円の+と-が逆転して電位の絶対値として最大を取っている)。



コメント