こんにちは。Horyです。
前回の記事では様々な物体の慣性モーメントを求めました。
今回の記事では前回の記事に関連して回転運動方程式の問題について考えたいと思います。
今回も頑張りましょう。
回転運動方程式
回転運動方程式に関してはこちらの記事でも解説しました。
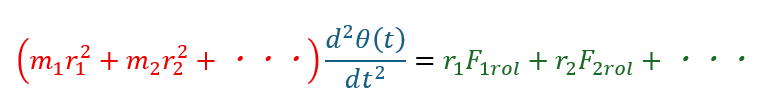
- 赤い部分・・・慣性モーメント
- 青い部分・・・角加速度
- 緑の部分・・・力のモーメント
ちなみに、物体が回転しないときは左辺の値が0になります。このとき、力のモーメントが釣り合っている状態であると言えます。
問題でも散々やってきましたね。
前回のおさらいですが・・・
- 物体の密度・・・ρ [kg/cm3]
- 質量・・・M [kg]
- 体積・・・V [cm3]
- ri[cm]・・・回転軸からの距離

まぁ、これらを用いて問題に取り組みましょう。
物体を坂で転がす
以下に示すのは色々なモノを坂で転がす問題です。

上に示す状況をテーマとした問題を実践します。頑張りましょう。
球殻の慣性モーメント
球殻の慣性モーメントを求めてみます。
基本的に3次元球面極座標を用いるのですが、球体と違う点は中身が空洞だと言うことです。
そのため、密度が異なってきます。

ここで、疑問ですが、上の式でrについて積分をしていませんがそれは大丈夫なのでしょうか?という点です。
よく考えていただきたいのですが、この物体は球殻であるという点です。
つまり、球体のように中身が詰まっていないのです(なかは質量がない・・・中心から距離がaの地点に質量Mの殻がある)。
そのため、球面座標のヤコビアンを用いることには用いるのですが、実質的にはrで積分をすることはないです(rにaを代入して終わり)。
並進運動と回転運動
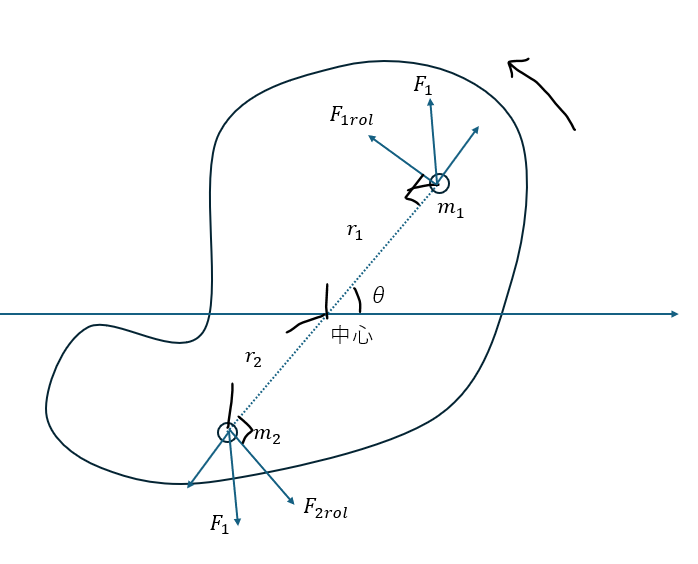
ボールは回転しながら斜面を転がっています。
ボールは回転運動と並進運動を行っていると考えることが出来ます。
- 回転運動・・・ボールの回転に関する運動方程式
- 並進運動・・・ボールの斜面方向に関する運動方程式
ここで、動摩擦力をfとして、角速度をωと考えます。
回転運動方程式ですが、上に説明した緑の部分は力のモーメントです(基準点をボールの重心とします)。

ここで重要なのはボールが回転しているという点です。
基本的に「斜面を滑ること」と「斜面上を回転する」ことは同時に起こりません。
そのため、並進運動の速度は角速度から導ける速度と等しくなります。
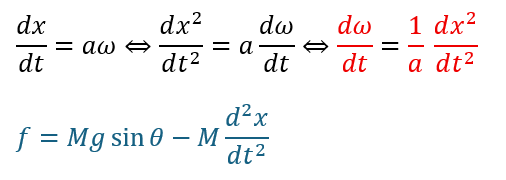
上の二式を回転運動の方程式に代入してみます。
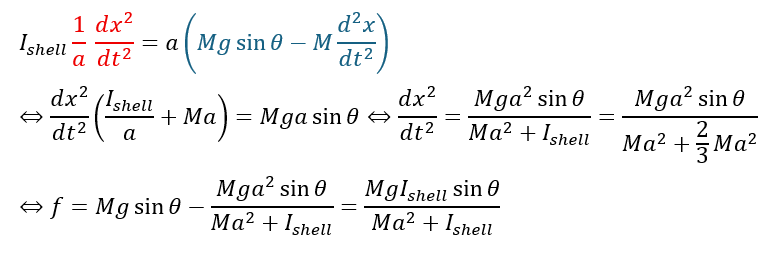
回転と並進の運動エネルギー
上の項で加速度が求まったので積分して速度を求めることができます。

ここで、回転運動のエネルギーってどうやって求めんねん?って思いますが、エネルギー保存則を用います。
この運動はボールが回転しながら坂を転がります。
そのため、坂を転がって位置エネルギーが下がった分が並進と回転のエネルギーとなります。

ボール以外の物体を坂から転がす
ボール以外の物体を坂から転がすことについて考えてみます。
- 半径aで質量Mのおにぎりを転がす
- おにぎりは完全な球体
- 転がっているときに崩れないモノとする
- 半径aで質量Mの太巻きを転がす
- 太巻きは完全な円柱で長さL
- 転がっているときに崩れない
- 半径aで質量Mの卵を転がす
- 卵は完全な球体
- 卵の中身は液体で満たされていると考えてよい
- 殻の質量を無視して転がっているときに割れない
それぞれの慣性モーメントを求めてみましょう。
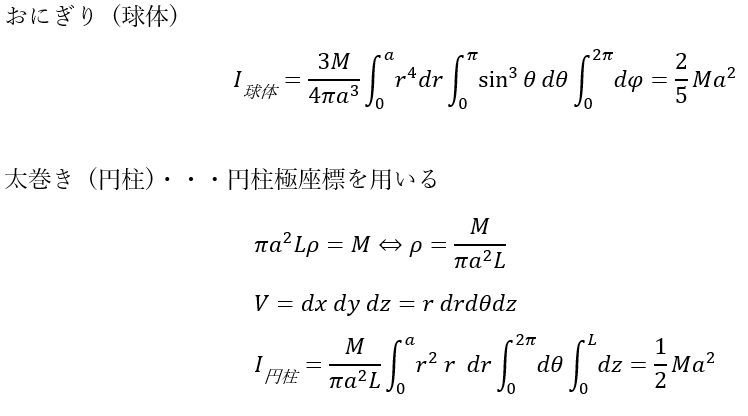
- 卵 (内部が液体)
- 殻は質量0と見なせる
- 水などの流体は回転しない
- 内部に流体が入った物体の慣性モーメントは0
- I(流体)=0
同じ質量と半径ならボール・おにぎり・太巻き・卵のどれが一番早く転がるのかを考えてみましょう。
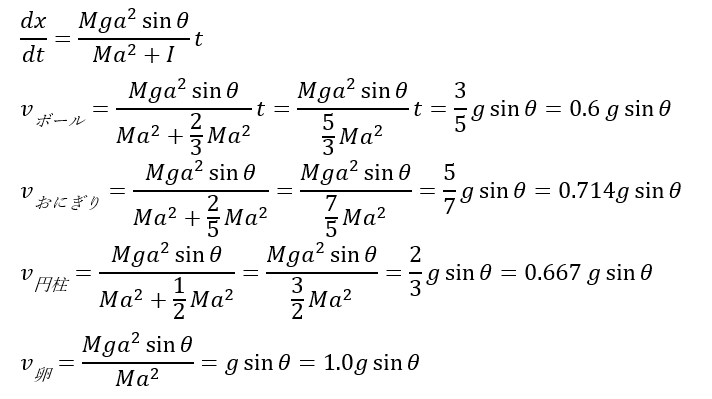
上のことから同じ時間で比較すると卵の速度が最大になります。
考えてみれば当たり前ですが、回転しない方が全部のエネルギーが並進運動に用いられるので速度は速くなりますよね。



コメント