こんにちは。Horyです。
前回の記事ではヤコビアンを用いた積分変数の変換について解説しました。
この記事では様々な物体の慣性モーメントを求めてみたいと思います。
前回までの記事を読んでいることを前提として書いていますので極座標やヤコビアンについて理解しているモノとして解説します。
今回も頑張りましょう。
慣性モーメントとは?
慣性モーメントとは簡単に「物体の回転のしにくさ」や「回転している物体の回転の止めやすさ」を表す量です。
慣性モーメントは物体そのものの重さや回転軸からの距離に依存します。
文字の定義を以下のよう定義します。
- 物体の密度・・・ρ [kg/cm3]
- 質量・・・M [kg]
- 体積・・・V [cm3]
- ri[cm]・・・回転軸からの距離

- 赤い部分・・・物体の微小部分の慣性モーメントを足し上げる
- 青い部分・・・rを半径として質量で積分した量と同じ (赤の言い換え)
- 緑の部分・・・dmを密度と微小体積で言い換える (青の言い換え)
まぁ、これだけではピンとこないと思うので図に示します。
上の赤い部分が何故、慣性モーメントになるのかはこちらの記事で解説しているので読んでおいてください。
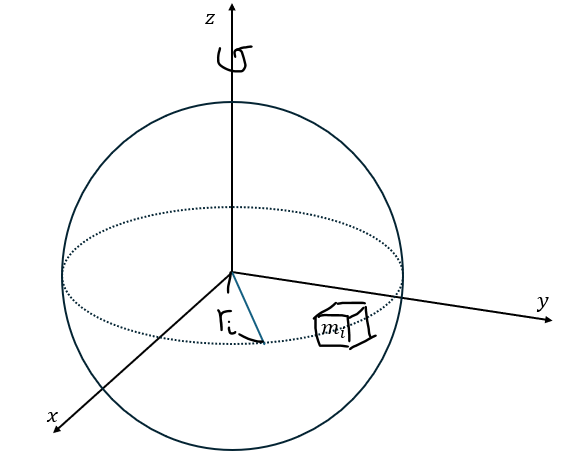
これでも意味分かんないと思います。
だって、赤い部分から青い部分に変形するときに、物体の微小部分の慣性モーメントを足し上げるのに、急に回転軸からの距離rを質量で積分するって言うけれど・・・質量で積分したところで物体全部の慣性モーメントを求めれるの?という疑問です。
まぁ、ここら辺は問題を解くことで理解していきましょう。
棒の慣性モーメント
まずは、慣性モーメントで一番簡単な棒の慣性モーメントを求めていきたいと思います。
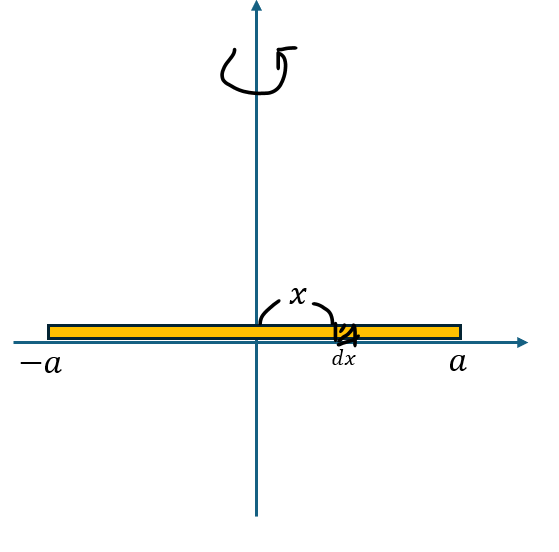
長さが2aで質量Mの細い棒の中心を通り、棒に垂直な軸に対して棒を回転させるとき、棒の慣性モーメントを求めます。
棒は非常に細いと見なして一次元で考えます。

以上が回答になります。
上の式変形の意味も分かったと思います。
距離の二乗を質量で積分することについて、dmの意味をよく考えて変形すると結局は距離で積分することになるので納得できると思います。
長方形の回転
正方形を回転させて、それぞれの軸周りでの慣性モーメントを求めていきます。
辺の長さが2a,2bの厚みが薄く、質量がMの長方形板の重心を通る対称軸について、この長方形板を回転させるときの慣性モーメントをそれぞれ求めろ。
厚みが薄いので二次元で考えて差し支えないです。
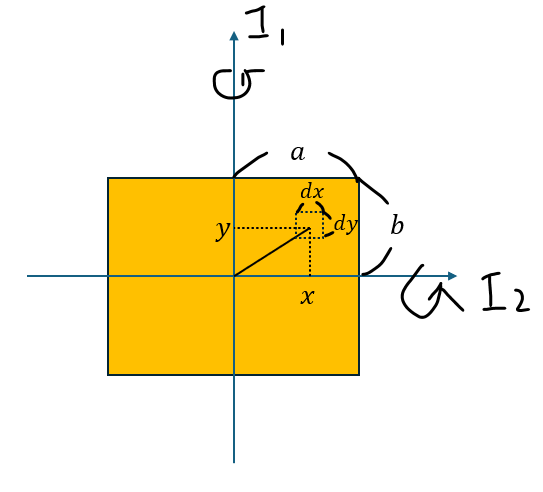
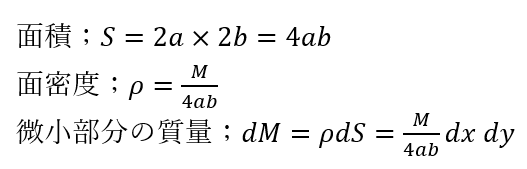
回転軸からの距離が回転軸によって何に変わるかをよく考えてください。
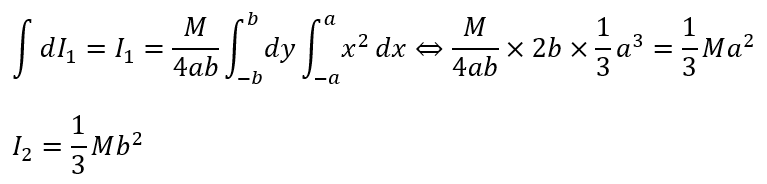
円板の回転
円板を回転させて、軸周りの慣性モーメントを求めます。
半径R, 質量Mの薄い円板の重心を通り円板の面に垂直な軸周りの慣性モーメントを求めてみます。
薄い円板のため二次元で考えてOKです。
この問題ですがx-y平面で考えるのは非常に厄介です。
二次元極座標を使うのが効果的ですね。
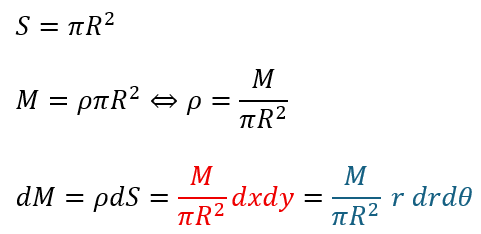
赤い部分のままだと何が厄介かというとxとyの範囲が具体的に分からないので積分範囲を考えるのが難しいという点です。
一方で、極座標であれば・・・
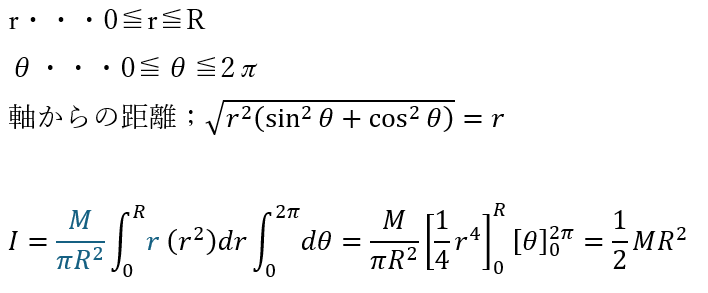
ここで、宿題を出しますが、上の円板をx軸やy軸周りに回転させるときの慣性モーメントを考えてみてください。
ヒントですが、三平方の定理をよく考えて最初に紹介した赤い式(Σのある式)に代入してみてください。
対称性があることも考慮すると・・・
また、以下の図に示すような中心に穴が空いた円盤の慣性モーメントも求めてみてください。
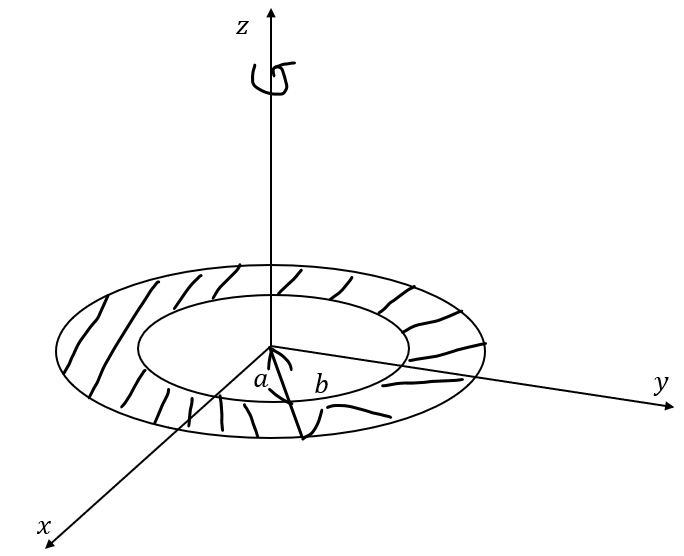
まぁ、やり方は変わりませんが、表面積が変わるので・・・
球体の慣性モーメント
最後に球体の慣性モーメントを求めてみます。
半径がRで質量がMの球体に関して、球の重心を通る回転軸について球を回転させる。
慣性モーメントを求めろ。
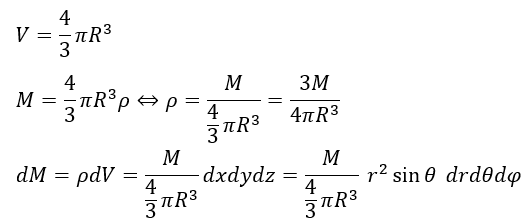
この問題についてもx,y,zだと範囲が厄介なので球面極座標で考えた方が良いです。

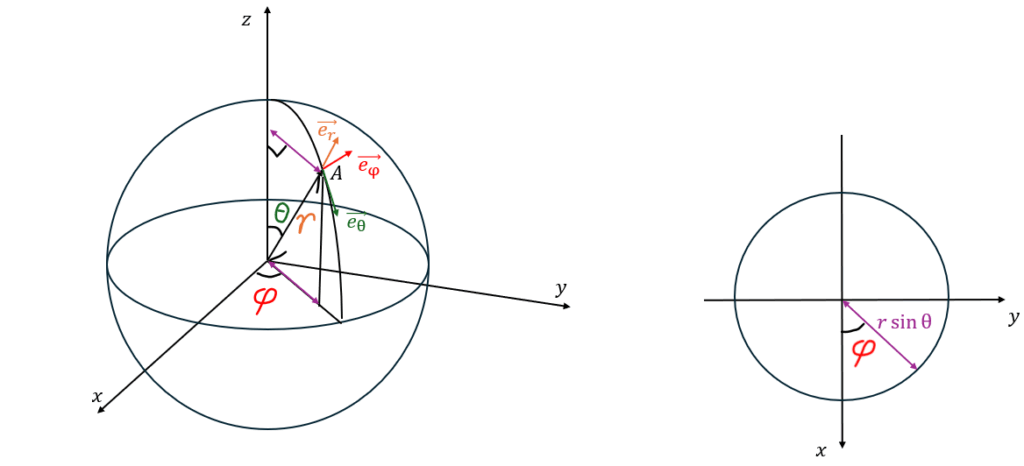
軸からの距離は上の図の紫色の矢印の長さですよね。
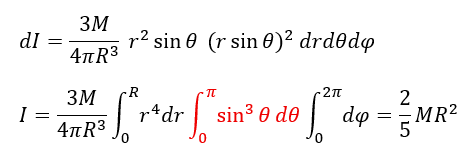
赤い部分は3倍角の公式で次数下げして計算してください。


