こんにちは。Horyです。
前回の記事では3次元極座標や写像に関して解説しました。
今回の記事では積分の変数変換とヤコビアンに関して解説します。
この記事は上に示した3つの記事の内容を理解していることを前提として書かれていますので読んでいない人は読んでおいてください。
本記事は今後解説する慣性モーメントを理解するためには必須の内容です。
今回も頑張りましょう。
積分の変数変換
積分の変数変換とは具体的にどういうことかと言うと・・・
微小面積や微小体積を直交座標で表すと以下のようになります。
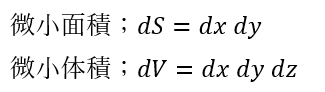
上の式は直交座標で表したものですが、これらを極座標にしたいですよね。
どういうことかというと・・・
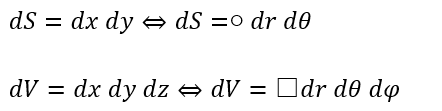
変数変換と言ってもそのまま変数変換が出来るわけではありません。
写像の記事でも話しましたが、直交座標と極座標では視点が違うためルールが違います。
そのため、つじつま合わせのために何らかの値を掛け算してあげないといけません。
上の式では何らかの値というのは○や□となっていますが、数学や物理の世界ではこの○や□のことをヤコビアンと言います。
次の事項ではヤコビアンを実際に求めたいと思います。
ただ、注意してほしいのが、本記事ではヤコビアンがどうしてそのような方法で求められるかの理由は解説しません。
理由として、解説するのであれば大学の線形代数学を解説しないといけないからです (ぼくのやる気があれば線形代数の分野を記事にするのでそこでまとめるかもデス)。
そのため、この記事ではヤコビアンをどのような演算で実際に求めるのかということを解説します。
二次元極座標のヤコビアン
二次元極座標のヤコビアンを求めます。
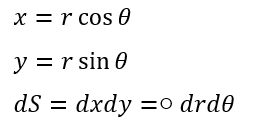
○を求めることが目的になります。
xとyをrとθで微分すると4つの項が出てきます。
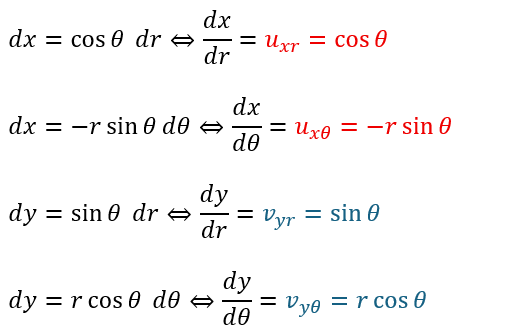
これを以下の図に示すように配置します。
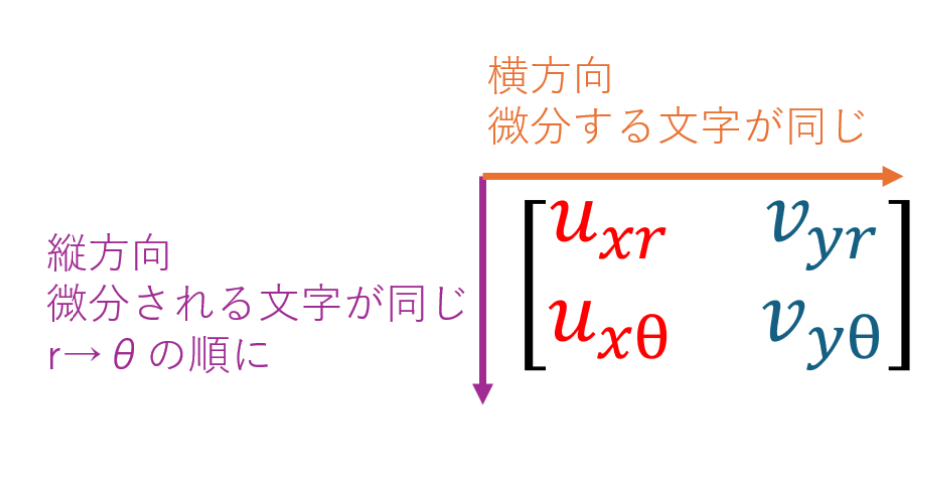
必ず上の手順に示すように配置してください。
上に示した式は2×2の行列式と呼ばれるモノです。
以下に示すのは行列式の計算方法です。
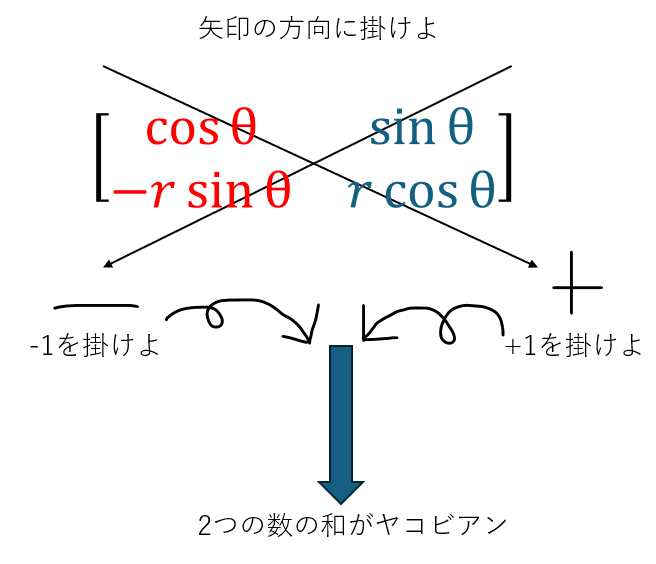
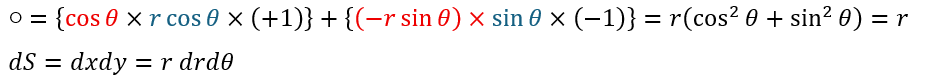
以上により二次元極座標への積分変数変換が完了しました。
3次元円柱極座標のヤコビアン
三次元円柱極座標のヤコビアンを求めます。
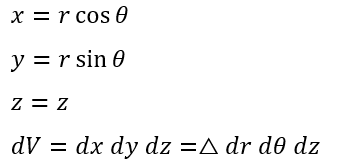
△を求めることが目的になります。
ただ、dzに関しては変数変換されないので結局はrとθだけになって二次元の場合と同じになるので・・・
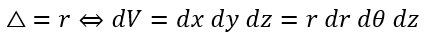
3次元球面極座標のヤコビアン
三次元球面極座標のヤコビアンを求めます。
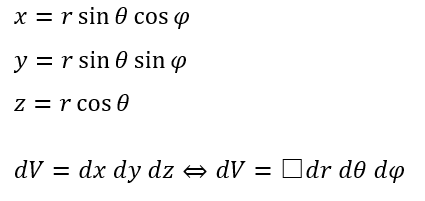
□を求めることが目的になります。
xとyとzをそれぞれr,θ,φで微分すると9つの項が出てきます。
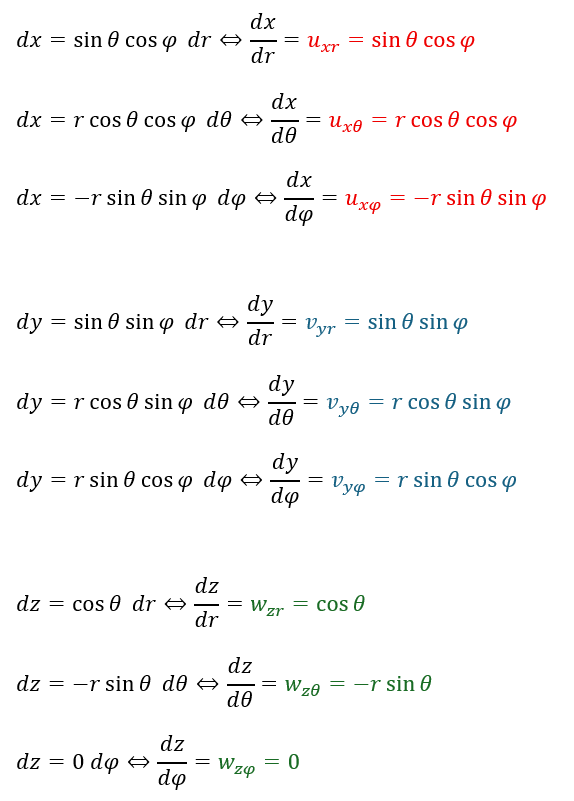
今度は3×3の行列式になります。作り方は2×2と全く同じです。
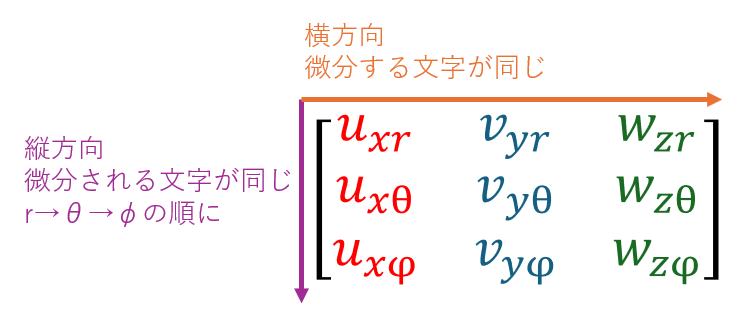
そして計算方法です。3×3の行列式の計算は以下のように行います。
これをサラスの公式と呼びます。
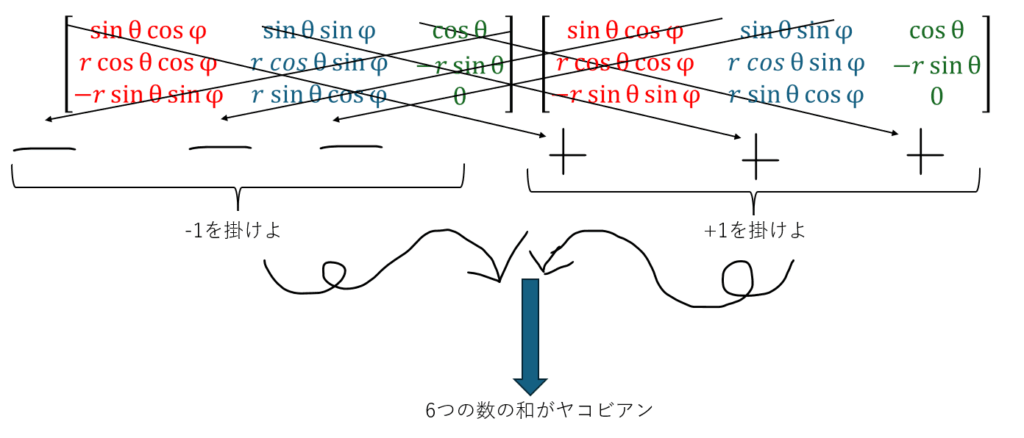
ちょっと大変ですが順番に計算します。

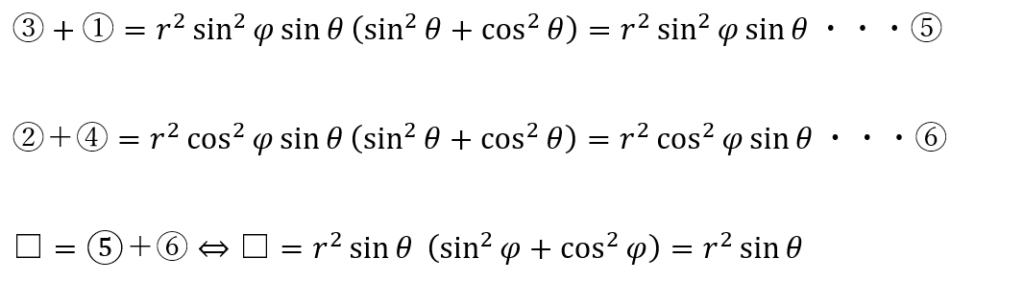
以上により3次元球面極座標のヤコビアンを求めることができて・・・
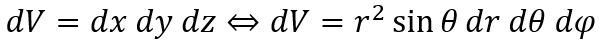



コメント