こんにちは。Horyです。
今回の記事では数学における写像について分かりやすく解説します。
今回の内容は後で記事にする積分の変数変換やヤコビアンに直結する内容であり、大学数学では非常に大切な数学の内容なので興味のある人は見といてください。
今回も頑張りましょう。
写像について・・・
写像に関して解説します。
- A 「写像?・・・」
- A 「何ですか写像って・・・」
- B 「ダメだこれ・・・」
- A 「写像って一般的に使わない言葉を知らなくてダメだこれって言われても(笑)」
上のようになってしまうかもなので「数学の写像」とはどういうことかをわかりやすい例 (問題)を用いて解説します。
以下に示すのは問題です。
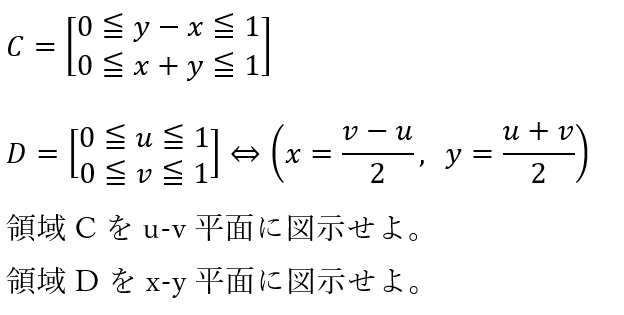
以下に示すのは解答です。斜線部がそれぞれCとDの領域になります。
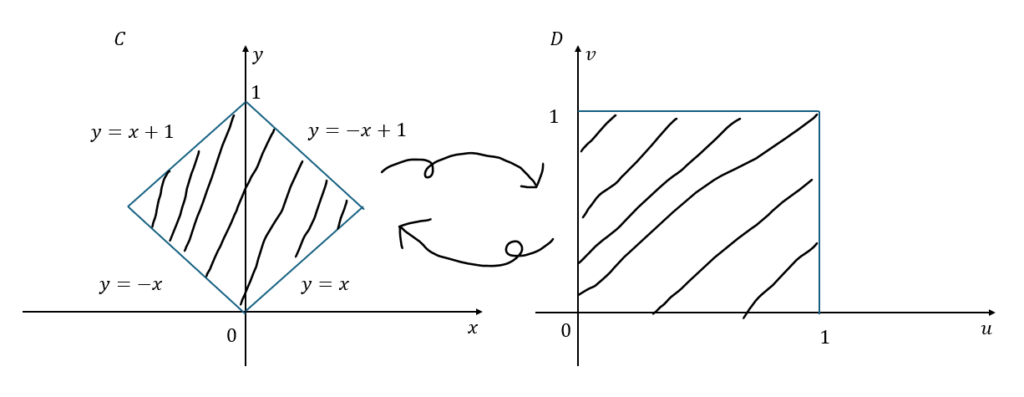
一応、このままでは何をやっているかよく分からないと思うので補足を加えます。
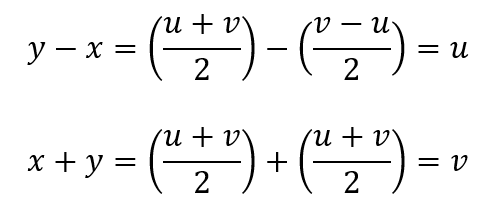
上に示すことから、領域CもDも言っていることは同じです。
ただ、領域Cはx-y平面、領域Dはu-v平面なので、図形が異なります。
- 領域Dは領域Cをu-vという変数をルールとして図示したときの写像
- 領域Cは領域Dをx-yという変数をルールとして図示したときの写像
つまり、写像とは「物事を異なる視点やルールから見たときにどう見えるか?」ということを意味していると思ってください。
例えば、現実に起きたニュースについて太郎と花子という別々の人間が考えることについて、考える対象は同じですが、それに関する解釈は異なりますよね。
上の例を先ほどの数学の問題で置き換えると・・・
- x-y平面(x-yというルール)・・・太郎の価値観から見た考え
- u-v平面(u-vというルール)・・・花子の価値観から見た考え
- 現実に起きたニュース (実際に起きた事実)・・・領域CもDも言っていることは同じ
- 太郎と花子で価値観が異なるので事実に対する解釈は異なる (領域CとDで図形が異なる理由)



コメント