こんにちは。Horyです。
前回の記事では3次元の極座標変換で直交座標と円柱極座標を解説しました。
今回の記事では直交座標と球面極座標の変換に関して解説します。
球面極座標に関しては暗記をしている人が非常に多いような印象を受けますが、正直、暗記をする必要なんて全くありません。
今回の記事では球面極座標の効率的な理解方法も踏まえて解説します。
今回の内容も大学内容です。頑張りましょう。
球面極座標
球面極座標とは直交座標に対して以下の図に示すように単位ベクトルをとった座標になります。
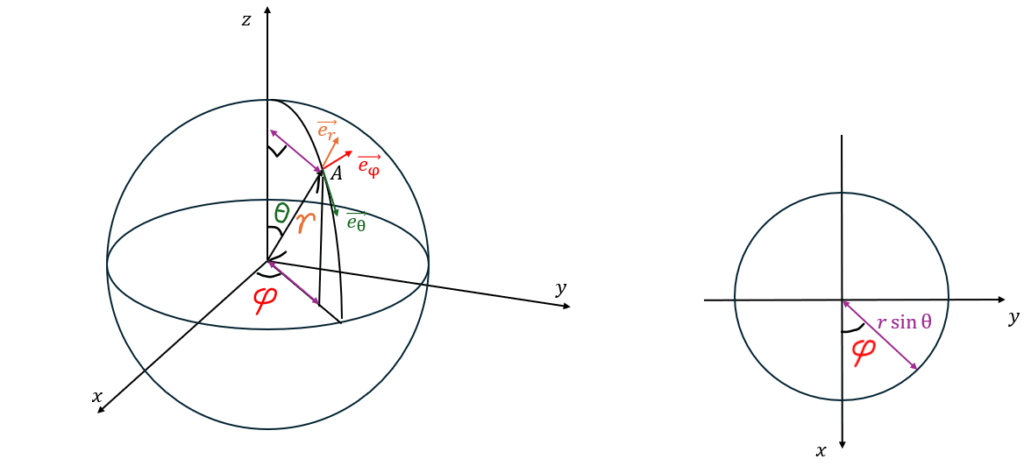
点Aの(x,y,z)座標を(r,θ,φ)で表します。
これを暗記する人が多いです(特にxとy座標)。
ただ、先に紫の矢印の長さを求めてx,y座標で二次元から見れば二次元極座標の場合に帰着できます。
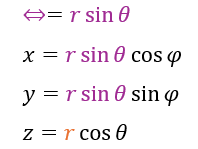
点Aの位置ベクトル
点Aの位置ベクトルを求めてみます。
これについて、原点から点Aに向かうベクトルは1つしかないので・・・
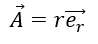
球面極座標→直交座標
球面極座標を直交座標系で表します。
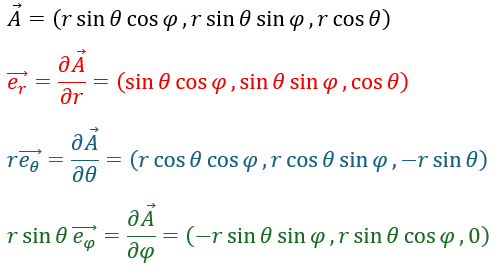
計算してみれば分かりますが、どの単位ベクトルも大きさは1です。
単位ベクトルの直交
単位ベクトルが直交している事を示すため内積を計算します。
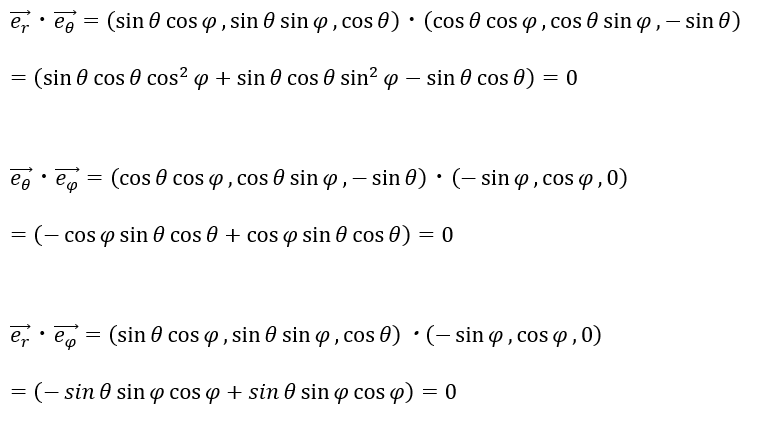
以上により内積が0になるので単位ベクトルは互いに直交しています。
速度ベクトル
速度ベクトルは位置ベクトルを時間で一回微分した量です。
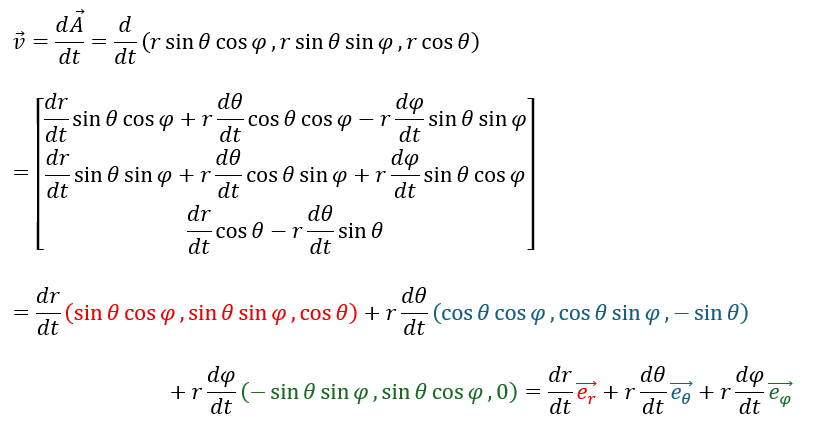
加速度ベクトル
加速度ベクトルは位置ベクトルを時間で2回微分した量です。
まぁ、計算をここに書くと非常に長くなるので一部を省略します。
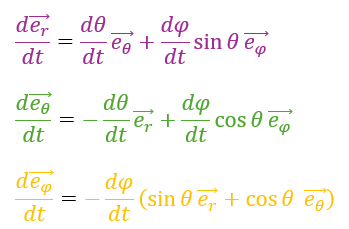
これを利用すれば加速度ベクトルを求めています。
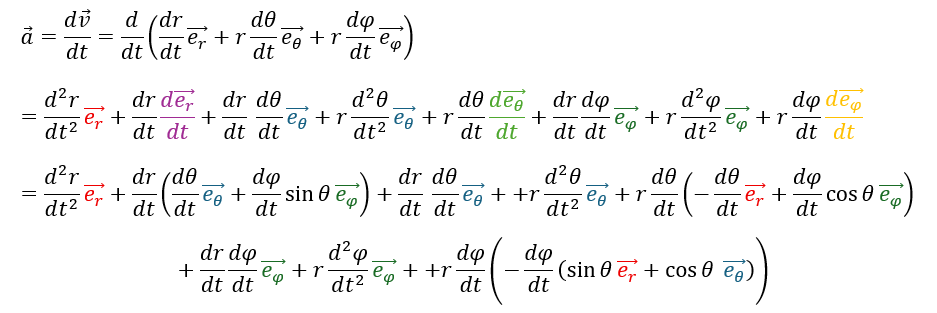
一応、計算は以上で終わりです、後はこれらをそれぞれの単位ベクトルでくくって整理すれば見やすい解答になると思います。



コメント