こんにちは。Horyです。
今回の記事では実験室系と重心系に関して話したいと思います。
正直に言うと、私は「ある理由」があって力学のこの分野の記事を書くことをためらっていましたが、連成振動は問題としても出ることはあるので解説します。
今回も頑張りましょう。
実験室系と重心系
実験室系と重心系と聞いて何のことかと思いますが、簡単に言えば慣性系と非慣性系と同様に物体の運動をどの視点から見るかの違いです。
- 実験室系・・・(基本的に)動かない座標から運動を見る (静止した水平面から)
- 重心系・・・系の重心から物体の運動を見る
基本的に実験室系でも重心系でも問題を解くことは可能です。
ただ、世の中には「重心系を使った方が楽だからこういった問題は重心系で解いた方が良い」のような考え方を持つ人がいます。
確かに、重心系で問題を解いた方が式の数や演算の数が減って楽なのかもしれません。
しかし、物理を初めとした自然科学の原理・法則にテクニックはありません。
上に示すことは「異なる視点や考え方を比較して優劣をつけること」に該当します。
そのような考え方をする人が一定数出てくるためこの事項を解説することをためらっていました。
重心系と実験室系に優劣はありません。
視点の違いによる解き方の違いを理解してどちらの方法でも出来るようにしてください。
連成振動の問題
以下に示すのは連成振動の問題です。

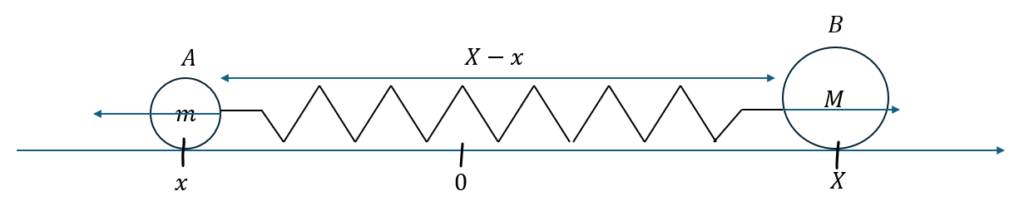
予想できると思いますが、この運動はバネがぶにゃぶにゃ伸びたり縮んだりしながら運動します。
そのため、どちらの物体も単振動を行うと予測できます。
実験室系で解く
地上のどこかに原点Oを設定して動かない座標(実験室系)から運動方程式を立てます。
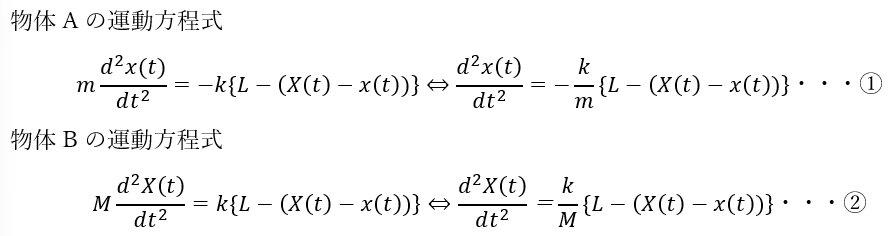
ここで、②から①を引き算します。
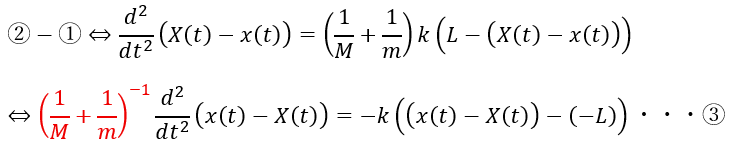
ここで、①と②を足します。
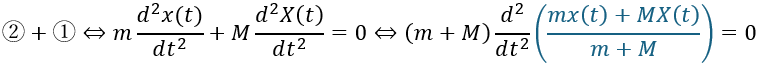
- 赤い部分・・・換算質量
- 青い部分・・・重心の位置
- ③・・・単振動の式になっている
- ④・・・重心の運動方程式
- 重心の加速度が0 ⇔ 重心の速度は一定 ⇔重心は等速で運動する
単振動に関しては以下の記事に記述したのでこの記事では原理から解くことはしません。
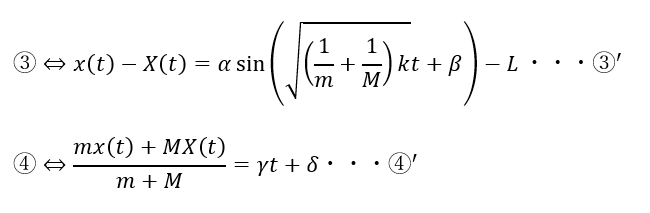
③’と④’を連立させることでそれぞれの物体の位置座標の関数を得れるので運動に関して議論が出来ます。
重心系で問題を解く
重心系で問題を解きます。
先ほどの説明で重心の速度が常に一定ということが分かりました。
重心と共に等速で動く座標系から運動を見ます(ちなみに、重心系は非慣性系ではなく慣性系です。止まっている座標系か等速で動く座標から考えることが慣性系)。
簡単のために、物体の重心の位置を原点0に取ると、座標は重心と共に等速で動くので重心の位置が常に0に固定されます。
補足ですが、実験室系だと④’から、実験室系だと重心の位置は動いています(0になってないから)。
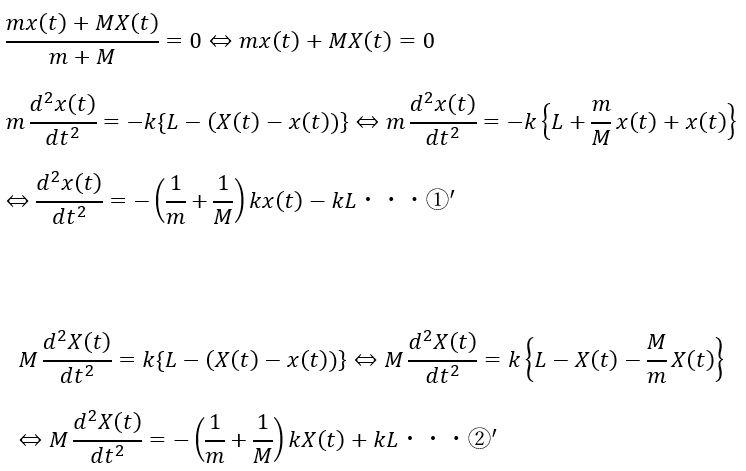
上の①’と②’を解けば物体の位置座標の関数を得れるので運動に関して議論が出来ます。
結局、どっちの方法でやっても単振動になることが分かりますね。



コメント