こんんちは。Horyです。
久しぶりに力学の分野に戻ってきましたが、いくつか取りこぼした問題があるので今後はそれらの問題をいくつか紹介します。
今回紹介するのは摩擦力と作用・反作用に関する問題です。
作用・反作用の法則に関してはこちらの記事で解説しました。
作用・反作用の法則と力の釣り合いは混同しやすいので必ず区別できるようになってください。
今回も頑張りましょう。
問題
以下に示すのは摩擦力に作用・反作用の法則が絡んだ問題です。

この問題を例に解説します。
摩擦力に関する記事はこちらに示すとおりなので見といてください。
(2)について、加速度と書いてありますが「加速度の大きさ」としてください。
(3)については、t=0sで物体は右端にあるとしてください。また、板の長さをLとします。
- 垂直抗力・・・N
- 摩擦力・・・接触する2固体の表面が相互運動を行うときの抵抗力
- 静止摩擦力・・・板について動き出すまでの抵抗力
- 最大摩擦力・・・板について動き出す時の抵抗力 = μN
- 動摩擦力・・・板について動き出した後の抵抗力 = μ’N
そして、注意しなければならないのが以下のことです。
- 運動を水平面(動かない座標系=慣性系)から見る
- 運動を板上(動く座標系=非慣性系)から見る
どちらの視点で解くかで考え方が大きく変わりますが、非慣性系で見ます。
考え方が大きく変わると言っても答えは同じになります。
慣性系と非慣性系に関する記事はこちらです。
問題を解く前の下準備 (1)の解答
まずは、問題を解く前の下準備です。
板と物体にかかる力を図示してみます。
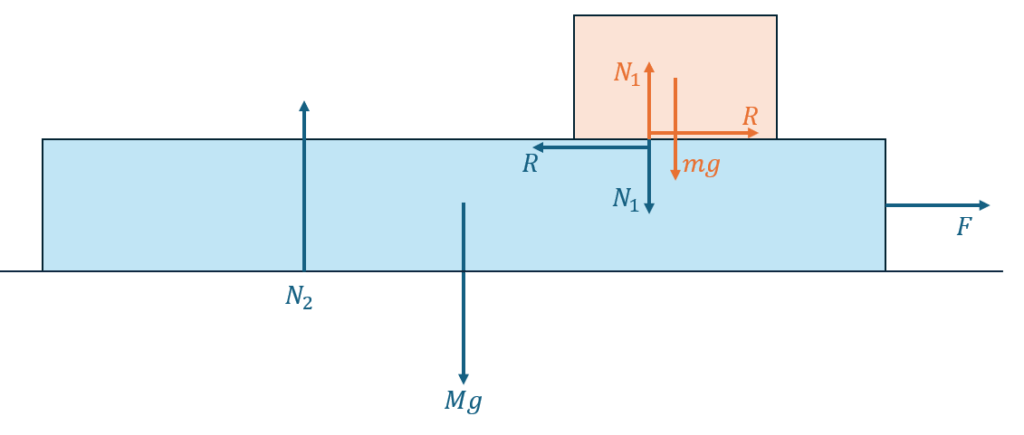
- 板に働く力 (青色の矢印)
- Mg・・・地球が板を引く力
- N2・・・接地面が板に与える垂直抗力
- N1(下)・・・物体が板に与える力 (板が物体に与える垂直抗力の反作用)
- R(左)・・・物体が板に与える力 (板が物体に与える摩擦力の反作用)
- 物体に働く力 (オレンジの矢印)
- mg・・・地球が物体を引く力
- N1(上)・・・板が物体に与える垂直抗力
- R(右)・・・板が物体に与える摩擦力
手順は以下に示すとおりです。
- ①;一体となって運動→加速度を求める
- ②;求めた加速度で小物体の運動方程式→最大摩擦力を考える
物体の進行方向(右)を正にしてスカラー表示で運動方程式を作ります。
加速度をαとします。
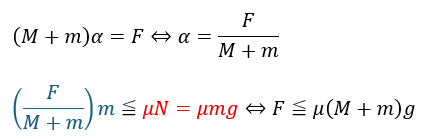
上の式の赤色の部分は物体が板を今にも滑り出すときの摩擦力です。
- 赤い部分・・・物体が今にも滑り出すときの摩擦力
- 青い部分・・・物体にかかる力
(2)(3)解答・解説
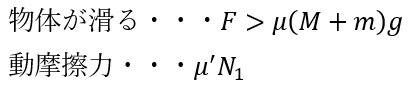
ここで、垂直抗力であるN1がよく分からないので物体と板について水平方向と鉛直方向で運動方程式を立てます。
- 物体の加速度の大きさ;β
- 板の加速度の大きさ;γ
どちらの運動方程式も板の進行方向を正とします。
ここで、疑問に思うのが、「物体は左に進むんじゃあないの?」と思うかもしれませんが、この考え方は板の上で物体を見たら正しいです(板の上という非慣性系上では物体は左に動く)。
静止する水平面上で板と物体を見ると板と物体はそれぞれ別の加速度で右方向(水平面上という慣性系ではどちらも右に動く)に動いています。
板と物体が別々の加速度で動いているために、物体はやがて板から落下します。

上の式で書かれている緑の部分と紫の部分は作用・反作用です。
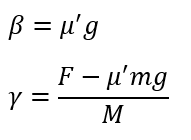
板に対する物体の相対化速度を考えます。ただし、右向きが正なので、進む方向がベクトル的にマイナスになることに注意です。
板に対する物体・・・物体の加速度から板の加速度を引く
- 右端の座標・・・0
- 初期速度・・・0
- 左端の座標・・・-L
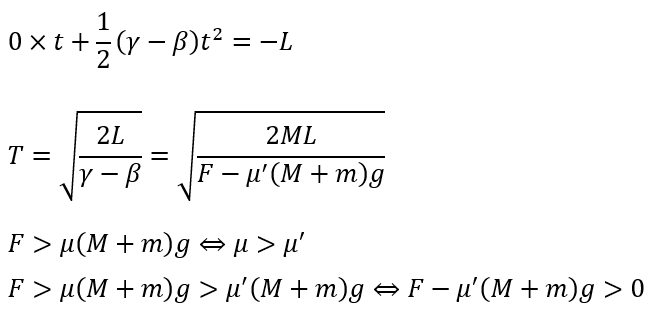
静止摩擦係数は動摩擦係数よりも大きいです。


コメント