こんにちは。Horyです。
今回の記事では波の反射に関して記事をまとめたいと思います。
波動の反射には2つの種類があって自由端反射と固定端反射というモノがあります。
入試では時間によって入射波と反射波による合成波がどうなっているかを答えさせる問題がよく出ます。
今回の記事の目的は波の反射の基礎を理解すると共に、入射波に対して反射波がどのように立式できるかを原理から解説したいと思います。
今回も頑張りましょう。
波の反射
「波の反射」という言葉を聞いたことはあってもどのような現象かを説明出来る人は非常に少ないと思います。
波の反射とは、例えば、「空気と水」や「空気と壁」のように素材(媒質)の異なる物質の境界に波動が達したときに、境界で跳ね返ることを波の反射と言います。
一方で、反射せずに通り過ぎることもあって、これを「波の透過」と言います。
波の透過に関しては次回の記事で解説します。
波の反射には2つの種類があります。
- 自由端反射・・・水面の波とかで起きる (プールの水が壁に当たるとき)
- 固定端反射・・・弦の振動とかで起きる
自由端反射について
自由端反射に関してまとめたいと思います。
入射波を以下に示すような式で記述します。
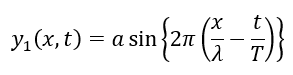
この入射波が「x=L」で自由端反射するとします。
まぁ、式だけで書いても分からないので図で示します。
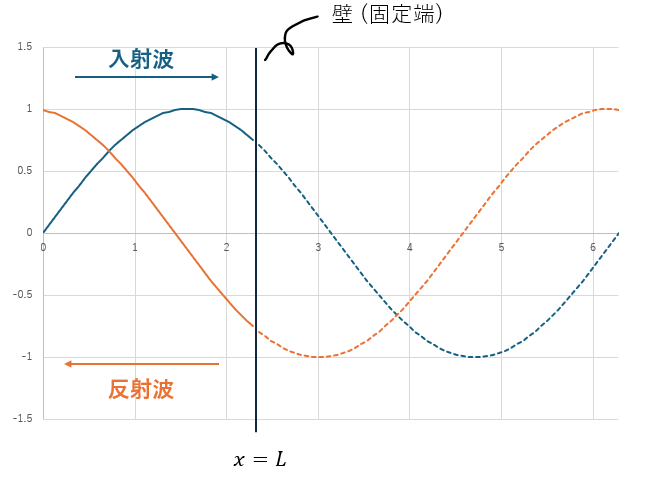
- 自由端反射
- 壁(境界)で波動を線対称に折り返す
- 反射波の進行方向は入射派と逆
- 反射波の位相は変化しない
次に上の図に示した反射波を立式してみます。

境界の反射波が位置xに届くまでの時間を考えて反射波を考えます。ただし、位相速度をCとします。
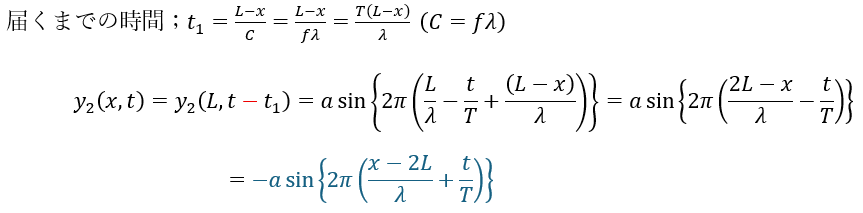
入射派と反射波を重ね合わせて合成波の式を立式してみましょう。
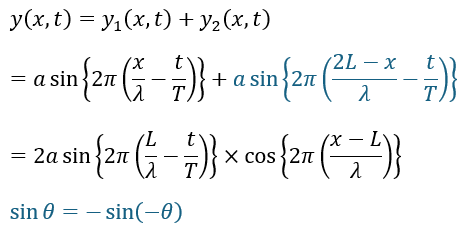
上の式から合成波は定常波になります。
上の合成波の式に「x=L」を代入するとcosの項が1になるので、境界での合成波の変位は最大で、定常波としては腹の部分になります。
三角関数の和積公式や定常波の式はこちらです。
固定端反射
固定端反射に関してまとめたいと思います。
入射波を以下に示すような式で記述します。
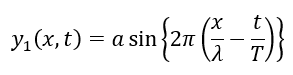
この入射波が「x=L」で固定端反射するとします。
まぁ、式だけで書いても分からないので図で示します。
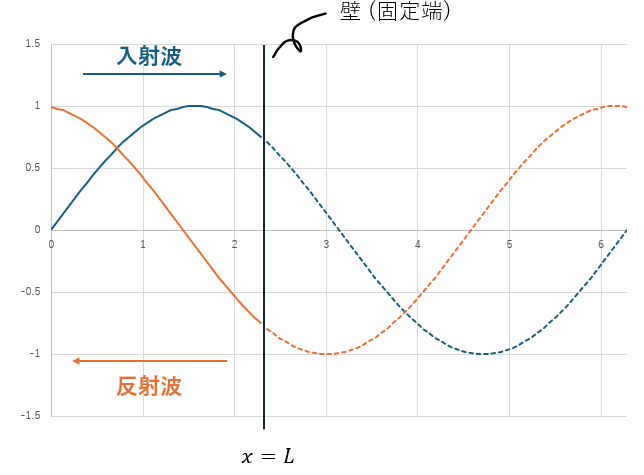

境界の反射波が位置xに届くまでの時間を考えて反射波を考えます。ただし、位相速度をCとします。

上の式から合成波は定常波になります。
上の式に「x=L」を代入すると、sinの項が0になるので、境界での合成波の変位は0となり、定常波として見れば節になります。


