こんにちは。Horyです。
前回の記事では波の干渉について意味と現象を理解しました。
今回の記事では定常波について解説しようと思います。
波の干渉と同様に定常波についても言葉を知っていても現象について説明できる人は少ないような気がします。
定常波の意味と現象を理解することが今回の記事の目的です。 今回も頑張りましょう。
定常波
定常波とは「進行方向が逆向きで位相速度(絶対値)が同じ波動が重ね合わさって出来た波」のことです。
2つの波動関数を立式します。
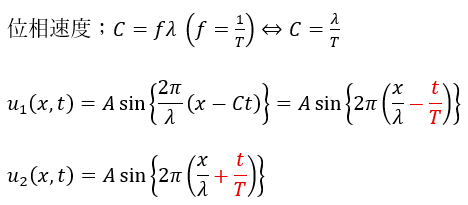
- 波動1;右向き(正の方向)に進行する波動
- 波動2;左向き(負の方向)に進行する波動
- 波の情報
- A;波の振幅
- λ;波長
- T;周期
正弦波の立式に関してはこちらの記事にも書かれている通りなので読んでおいてください。
重ね合わせてみる
上で示した2つの波を重ね合わせます。
重ね合わせの原理より単純な足し算を考えれば良いだけです。
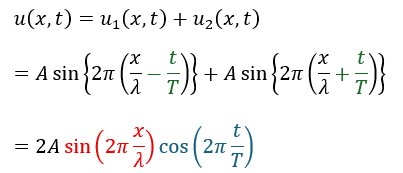
二段目から三段目の変形は三角関数の和関公式を用いています。この公式に関する記事はこちらなので読んでおいてください。
上のグラフを2つの方法で解釈することが出来ます。
- 位相と位置でグラフ→振幅が|2A×(赤い部分)| (青い部分は定数と見る)
- 位相と時間でグラフ→振幅が|2A×(青い部分)| (赤い部分は定数と見る)
重要なのは3段目の式における位置が出てくる部分(赤い部分)に位相速度に関する項 (t/T)がありません。
そのため、重ね合わせによって出来る合成波は(横に)移動せずに上下に振動していると言うように解釈できます。
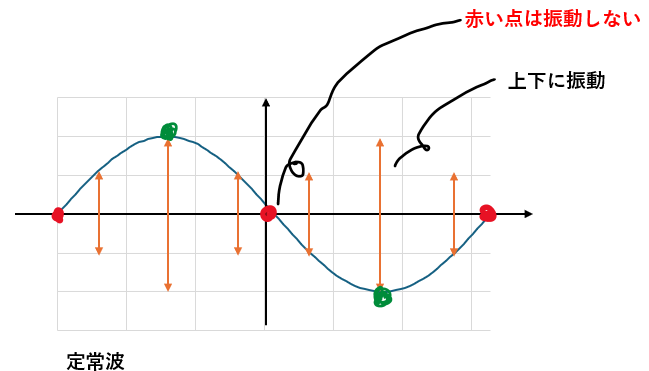
- 赤い点・・・常に振動しない→節と呼ばれる (節は半波長ごとに登場)
- 緑の点・・・最大の変位を与える(振動が最も大きい)→腹と呼ばれる
以上の事から定常波とは「進行方向が逆向きで位相速度の絶対値が同じ波動を重ね合わせた時にできる上下方向に振動する合成波」であることが分かります。



コメント