こんにちは。Horyです。
前回の記事ではフーリエ展開について解説しました。
この記事ではどんなに複雑な波動であっても周期性が確認できるのであれば、その波動は三角関数の級数で表せることを学びました。
また、上の記事から全ての周期性がある波動関数は正弦波の級数で表せることも言えることが分かりました。
今回の記事では波の干渉に関して解説します。
「干渉」という言葉を知っていたとしても現象を正確に答えれる人は理系でも少ないと思います。
今回は波の干渉について意味と現象を正確に理解することが目的です。
今回も頑張りましょう。
波の干渉について
波の干渉とは、「進行方向が同じ方向で位相速度も同じ正弦波の重ね合わせ」です。
実際に考えてみます。
以下のように2つの異なる波動関数を立式します。
立式方法はこちらの記事でも解説したとおりです。
- 2つの波動の共通点
- 進行方向が同じ
- 位相速度が同じ
- 2つの波動の相違点
- 波源(波の発生する場所)が異なる。
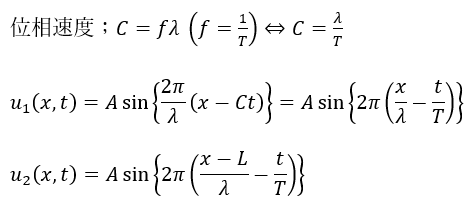
- 波の情報
- A;波の振幅
- λ;波長
- T;周期
- 波動2の波源は「x=L」の位置⇔単なる平衡移動
平衡移動については数学のこちらの記事にも解説がありますので分からなければ読んでおいてください。
重ね合わせてみる
波の干渉とは上に紹介した2つの波の重ね合わせのことです。
重ね合わせの原理から単純に足し算で考えれば良いです。
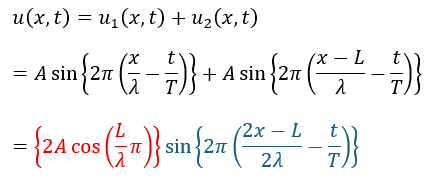
式の2段目から3段目の変形はは三角関数の和関公式を用いています(和関公式は数学の入試問題でも出ますので原理を理解してください。「和→積」が出来ない人が多すぎる印象を受けます)。
和関公式に関する記事はこちらですので読んでおいてください。
上の色が付いている部分を解説すると・・・
- 赤い部分・・・合成波の振幅を表す
- 青い部分・・・正弦波の式
つまり、干渉波は赤い部分の振幅の大きさの正弦波を表します。
ここで、波2の波源の位置を考えてみましょう。
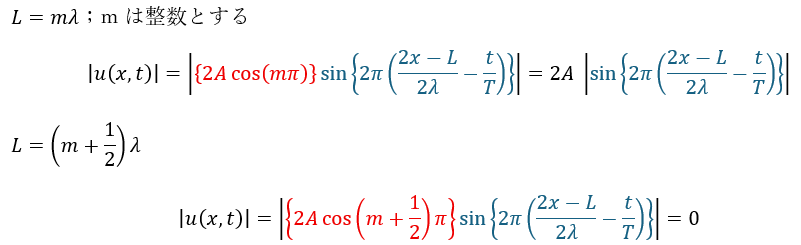
上のことをまとめると、波源の距離の差 (位相差)について・・・
- 位相差が波長の整数倍・・・波は強め合う
- 位相差が波長の半整数倍⇔(m+1/2)λ・・・波は弱め合って変位は0になる
以上のことをまとめると、波の干渉とは「進行方向と位相速度が同じで波源が異なる波が重ね合うことで波が強め合う点や弱め合う点が発生する現象」と言うことが出来ます。



コメント