こんにちは。Horyです。
前回の記事では波動方程式の解を求めると共に、その解の意味を解釈しました。
今回の記事では波動の形を簡単にまとめると共に高校物理で触れることが非常に多い正弦波(sinカーブ)について解説します。
今回も頑張りましょう。
波動の形
波動の形は大きく二種類に分けられます。
- ①;周期波動
- ②;非周期性波動 (パルス)
以下に周期波動と非周期波動を図に示してみます。
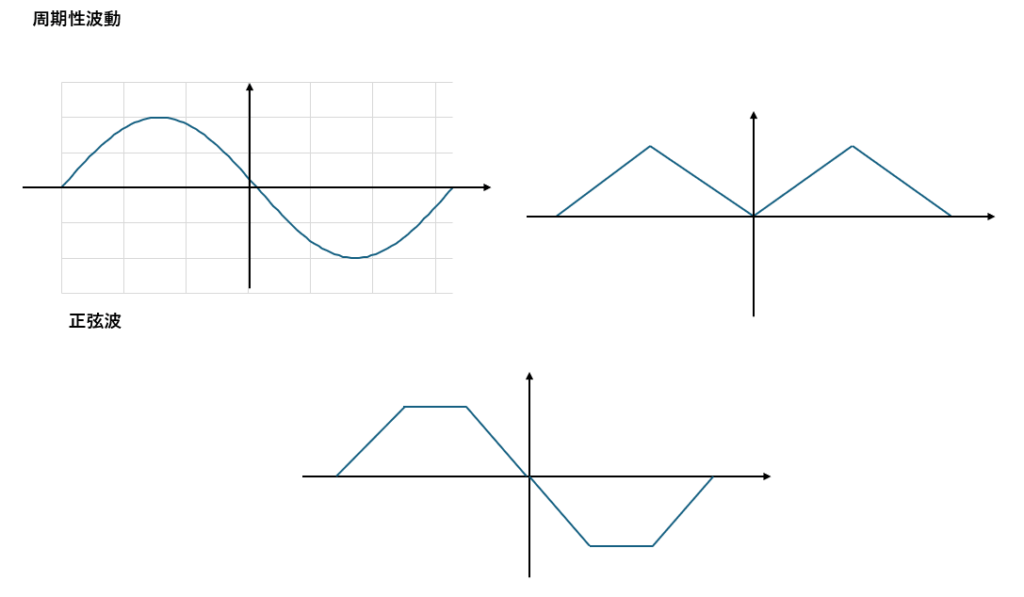
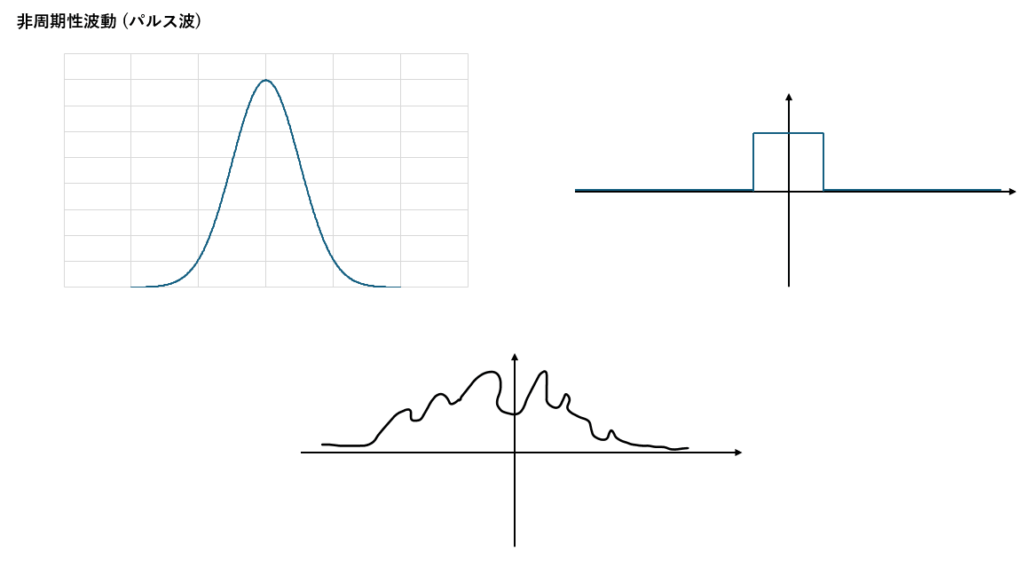
高校物理ではパルス波はほとんど出てきません。
出てくるのは周期性波動の正弦波(sinカーブ)です(だからといって、正弦波以外の波が出てこないとはかぎりません)。
正弦波について解説します。
正弦波の関数式とグラフ
正弦波の関数とグラフを示します。
正弦波とは三角関数の形の波が等速で伝達する現象です。
パラメーターを以下のように設定します。
- 振幅;A[m]・・・媒質の変位の最大値
- 波長;λ[m]・・・媒質の変位が同じ部分までの長さ
- 周期;T[s]・・・波長を位相速度で割り算した量 (波動が一波長分進行する時間)
- 振動数;f[1/s]・・・周期Tの逆数 (一秒での振動回数)
- 位相速度;C [m/s]
まぁ、言葉で説明するよりもグラフにした方が分かりやすいと思いますので二通りの方法でグラフにしてみます。
- グラフ①;距離と位相をグラフにする (t=0)
- グラフ②;時間と位相をグラフにする (x=0)
正弦波を関数に表すと以下のように表せます。

グラフに表してみます。ただし、2つのグラフで注意してもらいたいことがあります。
- A;振幅を1[m]に設定
- λ;波長を2π[m]に設定
- T;周期を1[s]に設定
- C =λ/T 2π [m/s]
- θ=π/6
- x-yグラフ・・・t=0[s]のを切り取っているモノとする
- t-yグラフ・・・x=0[m]のを切り取っているモノとする
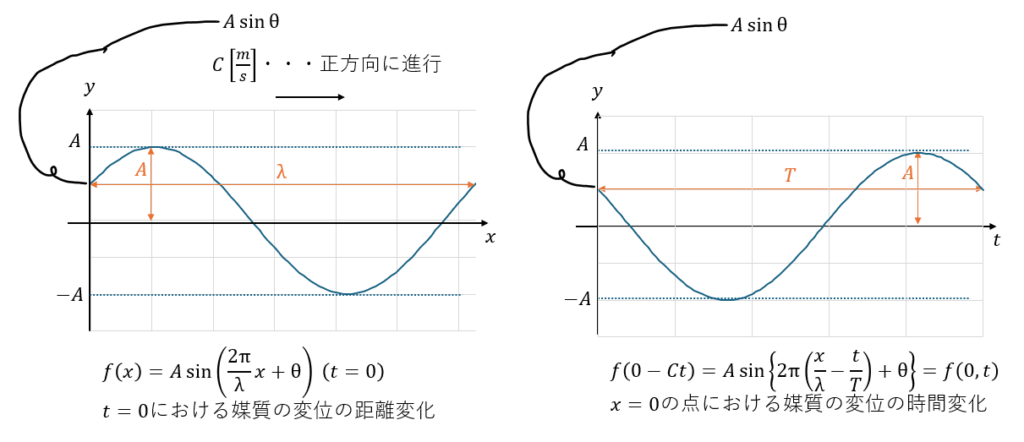
ちなみに、負の方向に進むのであれば、上の式の青い部分の符号を+に逆転すれば良いだけです。
もし、2つのグラフの対応がよく分からないのであれば、x-yグラフを右送り(正方向)に送ったときにx=0の点の媒質の変位はどのように変化するかを考えてみてください。
たくさんの学生を指導してきて、2つのグラフの対応がよく分からないと言うことがよくありましたので、、、


