こんにちは。Horyです。
前回の記事では熱力学での定積・定圧・等温変化に関して熱力学第一法則から内部エネルギー・熱量・仕事量に関して簡単に解説しました。
今回の記事ではこれらの条件で状態が遷移する問題に取り組みたいと思います。
サイクル過程の問題ではないです(サイクル過程の問題は別の記事で解説します)。
今回も頑張りましょう。
状態の遷移 問題
以下に示すのは今回紹介する問題になります。

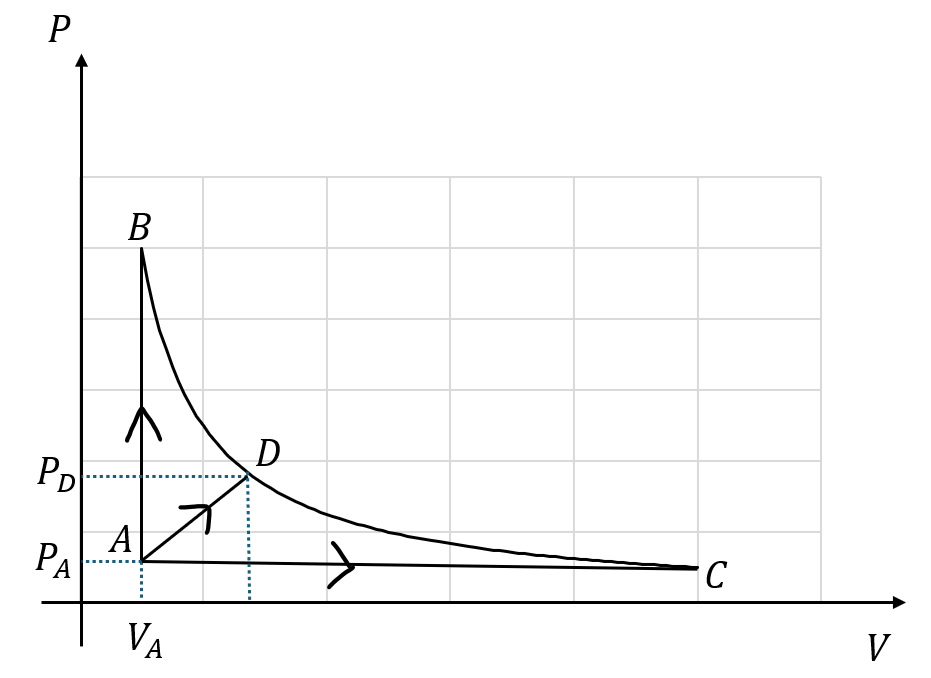
この問題を例に解説します。
注意してほしいのは理想気体であるかもしれませんが単原子分子とは限らないので定積モル比熱がCvと記載されています。
ここら辺の話はこの記事に書いてあるので読んどいてください。
また、主役と正の仕事を以下のように定義して熱力学第一法則を立式します。
- 主役;系(気体)
- 正の仕事;外部が気体にする仕事「+dW」
- 立式;dU= dQ – dW (マイナスがつくのは気体が主役だから)
- 求める仕事;気体が外部にする仕事
下準備はこんなところでしょうか?
頑張りましょう。
定積変化 (A→B)
定積変化について解説します。
まず、体積が変化しないので仕事量は0です。
そして、仕事量が0になるということは気体に与えられた熱量がそのまま内部エネルギーになります。
A→Bで温度は増加するので系の内部エネルギー変化も正です。
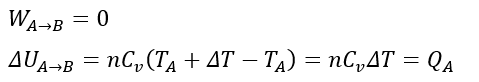
定圧変化 (A→C)
定圧変化について解説します。
まず、体積は増加しているので気体が外部にした仕事は正です(仕事は圧力を体積で積分する)。
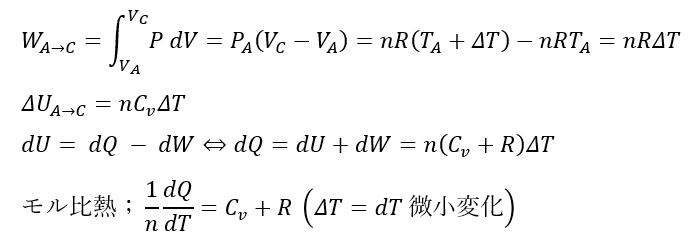
比熱は気体に流入した熱量を温度で微分したものです。
A→D
A→Dについては圧力と体積の比が一定の変化です。
まず、体積は増加しているので気体が外部にした仕事は正です(仕事は圧力を体積で積分する)。
A→Dの仕事量は以下の図の斜線部の面積です。
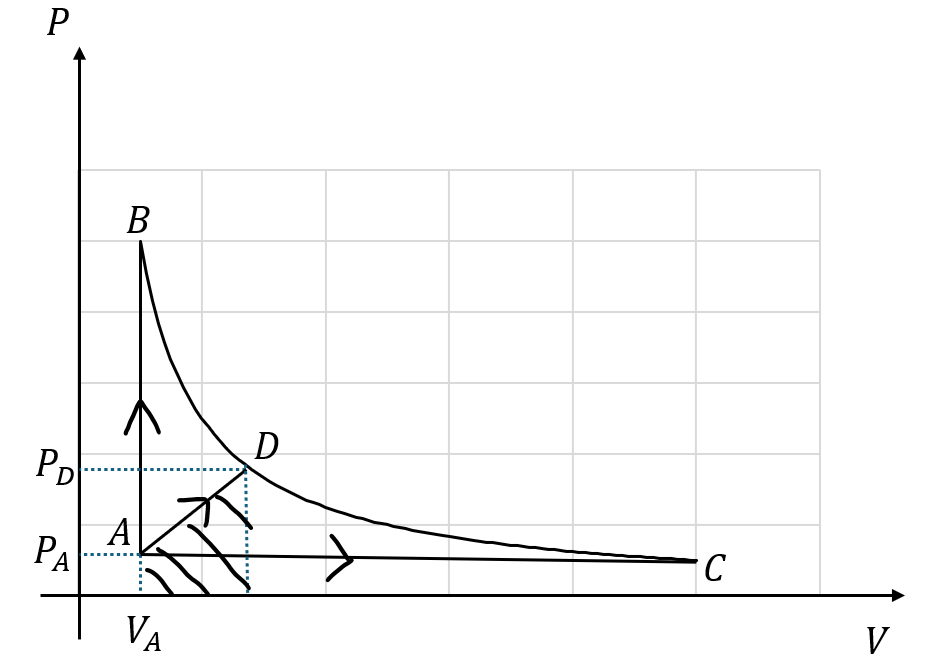
上に示す図の台形の面積が仕事になります。
A→Dにおける体積を変数とした圧力の関数を求めることはできなさそうなので積分は使えなさそうですが、グラフが直線であること(圧力と体積の比が一定)から圧力が体積の一次関数であることは分かるので仕事を何とか求められそうです。
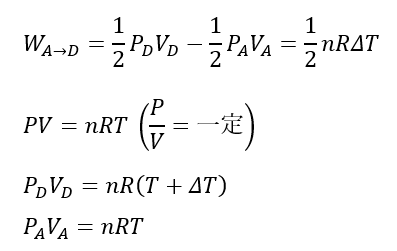
気体がした仕事を求めることはできたので後は熱と内部エネルギー変化のみです。
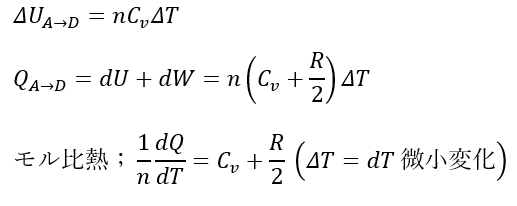
圧力の記述がない問題
上で紹介した問題と同様の問題ですが、圧力の記述がない場合もあります。
以下に示す問題を解いてみましょう。

この問題を例に解説を行います。
V1<V2なので膨張します。
そのため、気体がした仕事は正と見ることができます。
圧力の記述がないですが、状態方程式を使って体積で表せばいいだけです。
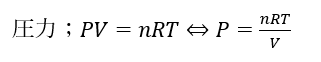
- A→B・・・定積変化
- B→C・・・等温変化
- A→D・・・等温変化
- D→C・・・体積一定
A→B→Cの変化
この変化について考えてみます。
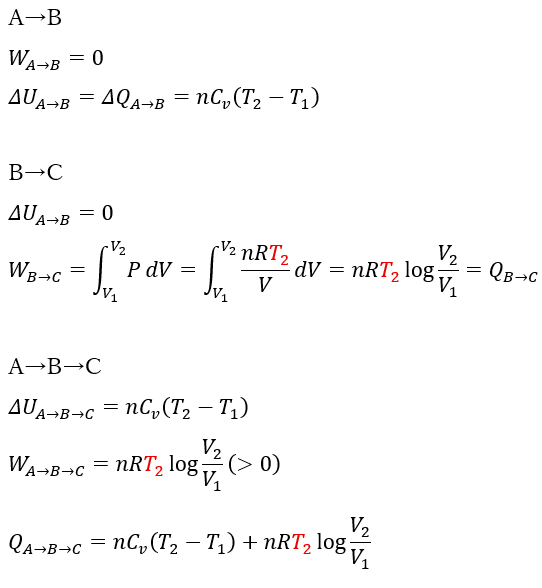
A→D→Cの変化
この変化について解説します。
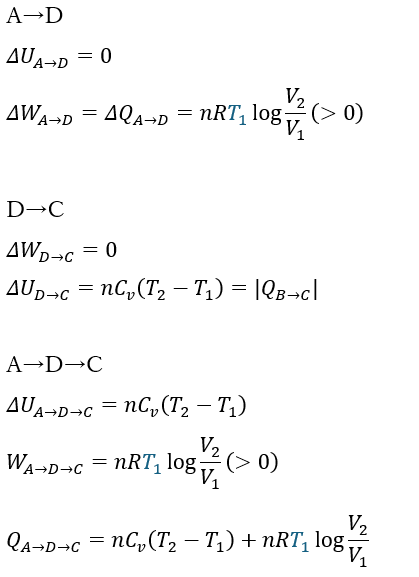
考察
最後にこの問題の考察を行います。
この問題は「A→B→C」と「A→D→C」共に始点がAで終点がCとなる問題です。
- 内部エネルギー・・・どちらの経路でも変化なし
- 熱量・・・経路によって違いが出る
- 仕事・・・経路によって違いが出る
内部エネルギーは力学に出てくる保存力のように始点と終点が同じであればどんなルートを辿っても値が変化しません。
このように始点と終点の状態に依存する量を状態量といいます。一方で熱や仕事は経路に依存するので状態量とは言えません。



コメント