こんにちは。Horyです。
前回の記事では高校の気体化学で使う法則式を簡単にまとめました。
この中で気体の状態方程式について解説しました。その中の注意で紹介した式は理想気体で成立する式でアルコとも説明しました。
今回の記事では、理想気体と実在気体の違いを解説し、前回の記事で紹介した式を何故実在気体に当てはめてはいけないのかということも解説します。
今回も頑張りましょう。
理想気体の状態方程式
前回の記事の復習も兼ねて理想気体の状態方程式を記述します。
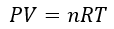
上の式に出てくる文字の定義をまとめます。
- P・・・容器中の全気体分子が壁を押す力
- V・・・気体分子の動くことのできる体積
- T・・・容器内の温度
- n・・・物質量
現実の気体(実在気体)で上の式を当てはめても本当に良いのかということに焦点をあてて解説します。
- T・・・問題なさそう
- n・・・問題なさそう
- V(容器の体積=気体粒子が動ける範囲)としているが・・・
- 気体粒子自体にも体積がある
- 体積をそのまま容器の体積に置き換えるのは現実の気体ではおかしい
- P(気体の圧力)としているが・・・
- 気体粒子間にも相互作用(分子間力)は存在する
- 現実の気体で圧力をそのままPにするのはおかしい
理想気体(PV=nRT)とは以下のような現実の気体ではあり得ないことを想定した場合の状態方程式です。
- 気体粒子感の分子間力を0としている
- 気体自体の体積を0としている
実在気体の状態方程式
ひとまず、理想気体と実在気体の違いを以下にまとめます。
- 理想気体
- 分子間力が0である
- 気体の体積が0である
- 気体の質量は0でない
- PV=nRTの状態方程式が成立
- 常に期待状態である
- 実在気体
- 分子間力が0でない
- 気体の体積が0でない
- 気体の質量が0でない
- PV=nRTは近似的に成立する
- 圧力Pや体積Vの変化で気体・液体・固体の状態変化
ここで、分子間力と気体粒子自体に体積があることがどのような効果を及ぼすかを考察します。
- 分子間力
- 分子間力は引力である
- 引力だから気体粒子同士が引き合う
- だから、分子間力が働かない時と比べて圧力・体積は小さくなる
- 気体粒子自体の体積
- 粒子自体に体積がある
- 気体の体積(気体が動ける容器の体積)は粒子数分の体積だけ大きくなる
- だから、気体自体の体積は動ける範囲を大きくする
だから、実在気体の状態方程式は理想気体の状態方程式に補正を加えて以下のように書けます。
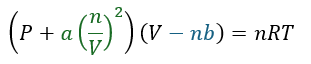
- 緑文字・・・分子間力の効果(圧力に補正)
- 青文字・・・気体粒子自体の体積効果(気体の動ける範囲に補正)
理想気体に近い気体
実在気体を理想気体の振る舞いに近づけたいときはどうすれば良いでしょうか?
分子間力と気体粒子自体の体積が原因と言うことを話しました。これの影響を押さえるにはどうすればいいか考えればいいわけです。
- 分子間力・・・要するに、着たい粒子同士の引き合う力
- 引き合う力を断ち切りたい⇔引きつけようとしても振り切るようにしたい
- だから、粒子の速度を上げる(熱運動を活発に)⇔温度を高温にする
- 気体粒子自体の体積
- 単位体積当たりに占める粒子数が少なければ体積0と見なせる
- だから、密度を低くする⇔壁への衝突回数が減る⇔圧力を低圧にする
以上のことから、実在気体を理想気体に近づけるには高温・低圧にすれば良いです。
理想気体と実在気体の比較
理想気体と実在気体を比較します。
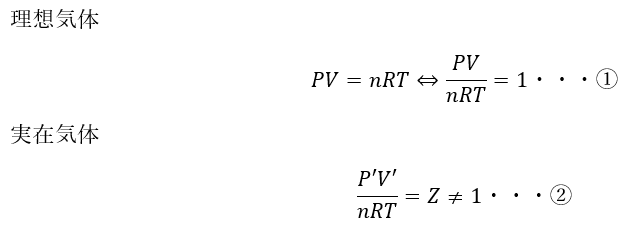
ここで、P(圧力)-Zグラフを考えると以下のようになります。
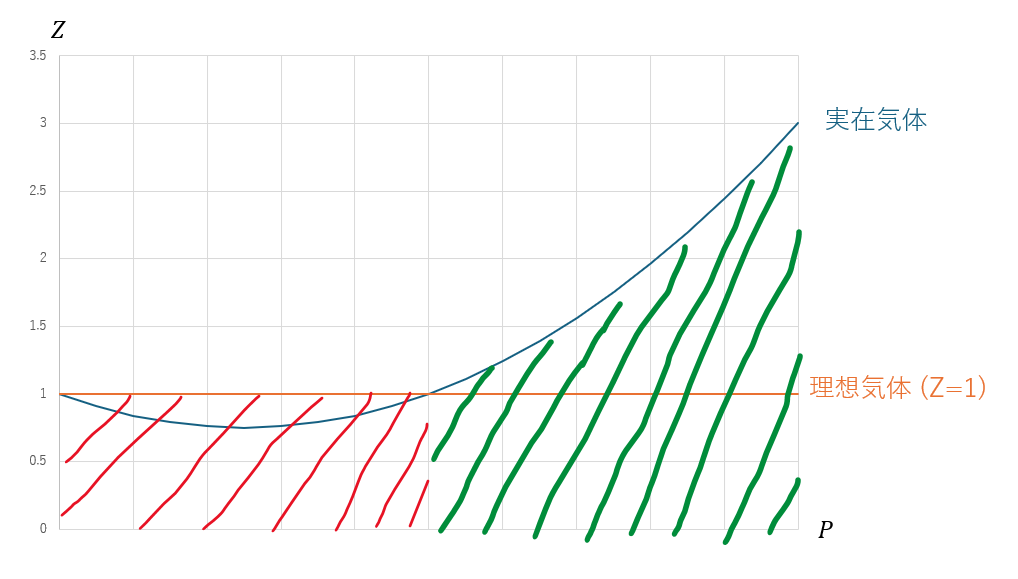
ここで、①と②の比を取ります。
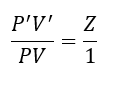
ここで、圧力が同じと仮定すると、P=P’として・・・

- 赤の領域・・・実在気体の体積が減少
- 緑の領域・・・実在気体の体積が増加
ちなみに、気体の中で理想気体に最も近いのは水素です。何故なら・・・
- 水素は元素の中で最も軽い・・・体積が0に近い
- 水素の分子間力が小さい・・・電子の数が少ない



コメント