こんにちは。Horyです。
今回の記事では気体化学の歴史を振り返ると共に、高校化学で使う気体に関する公式の原理をまとめていこうと思います。
今回も頑張りましょう。
気体化学の歴史
以下に示すのは気体化学の歴史になります。
- 大気圧の発見
- ボイルの法則の発見
- シャルルの法則の発見
- アボガドロの法則の発見
- 理想気体の状態方程式の発見
これらについて、個別に解説します。頑張りましょう。
大気圧の発見
トリチェリーとパスカルが大気圧を発見しました。
まず、発見の経緯となった実験のプロセスを以下に示します。
- ガラスパイプを水銀で満たす
- 容器に水銀を入れる
- ガラスパイプを逆さまに水銀の入った容器に入れる
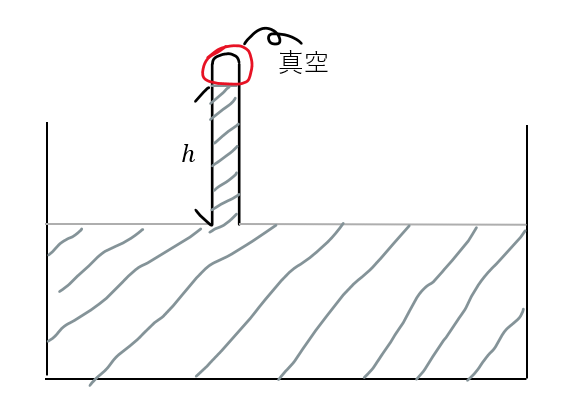
結果として、上の図に示すように、ガラスパイプの中に真空空間(トリチェリーの真空)ができて、大気圧下で実験を行うと高さhは約76cmになりました。
何故こんなことになるかを考えたときに、大気が容器に入った水銀の表面を押したと結論づけました。
そして、大気圧の定義(1 atm)を以下のように設定しました。
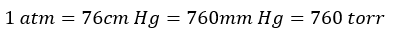
ちなみに、これを水で行った場合、高さは13.6倍になります。
ところで、何故、上の水銀の単位が現在使用されていないかというと、水銀(Hg)は温度で密度が変わりやすいです。
だから、これの代わりにPa(パスカル)という単位を用いて・・・
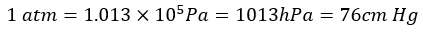
というように圧力を設定しました。
ボイルの法則
ボイルの法則に関してデス。これは、気体の圧力をP[Pa]、体積をV[cm3]と考えると・・・
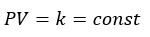
- 気体の圧力と体積の積が一定
- 気体の圧力は体積に反比例
これが、何故か説明するには気体分子運動論の説明になり、物理の内容になってしまうので、あくまでイメージで解説します(気体分子運動論については物理の記事で書きます)。
ピストンの中の粒子を考えます。
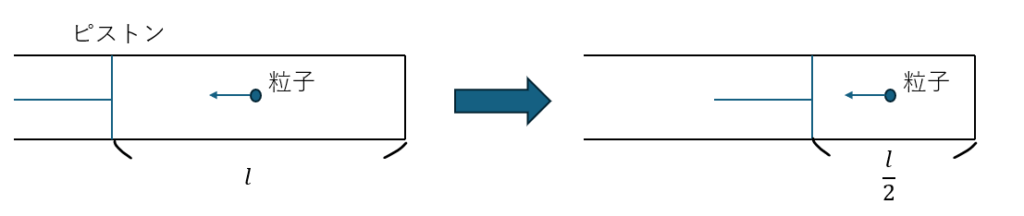
- ピストン内を粒子が一定速度で運動
- 圧力=粒子がピストン(壁)を押す時の単位体積あたりの力
- 長さが半分になる→単位時間に押す頻度が2倍→圧力も2倍に
このように考えます。物理の記事ではこのボイルの法則を真面目に証明します。
シャルルの法則
シャルル法則に関してです。気体の体積をV[cm3],温度をT[K]とすると・・・
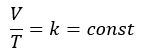
- 気体の体積と圧力の比は一定
- 気体の体積は気体の温度に比例する
ちなみに、容器内の物質量[mol]が一定であれば次のことが成立します。

体積が0になる時を考えてみてください。
T=-273℃になります。我々はこの温度を絶対零度と呼び、新たにT=-273℃を0[K]としました。K[ケルビン]による温度の表記を絶対温度による温度表記と言います。だから0℃=273[K]です。
これは、実験によって得られた結果で、高温から低温に冷やす過程での気体の体積の減少率を正確に測定したデータによる結果です。
ちなみに、ボイルの法則と合わせてボイル・シャルルの法則と呼んでいて・・・
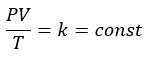
アボガドロの法則
アボガドロの法則に関してです。気体の体積をV[cm3]、粒子数をn[個]とします。
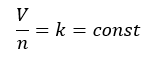
- 気体の体積と粒子数の比は一定
- 気体の体積は粒子数に比例する
ただし、注意があります。この法則が成立するのは同温・同圧であることが条件で、このときに、気体の種類によらず上の法則は成立します。
理想気体の状態方程式
理想気体の状態方程式です。これは、上で解説した全てのことを使います。

上に示した一定値Rを気体定数と呼びます。ちなみに、大気圧下で1molの気体の体積を22.4Lより
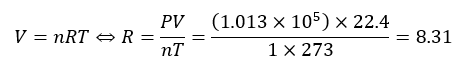
計算すると上の値になります。
注意してほしいのは、これが理想気体の状態方程式ということです。理想気体とは以下の条件を満たす気体です。
- 絶対零度で気体の体積は0になる
- 気体に分子間力が働かない
ここで、理想気体の状態方程式に出てくる文字の定義をまとめます。
- P・・・容器中の全気体分子が壁を押す力 (衝突による力積)
- V・・・気体分子が動くことのできる体積
- T・・・容器内の温度
- n・・・物質量



コメント