こんにちは。Horyです。
これまでの記事で、抵抗・コンデンサ・コイルが組み合わさった回路に関して電流の様子を式にして表しました。
まだやってない組合わせはコイルとコンデンサのLC回路になります。このような回路では電気振動と言う現象が起こります。
電気振動とは、コンデンサにたまる電荷が正や負に一定の周期で変動することです。
どういうことか分からないと思いますがやってみます。
今回も頑張りましょう。
LC回路
以下に示すような回路を考えます。
ただし、電池の起電力をV,コンデンサの容量をC,コイルの自己インダクタンスをLと考えます。そして、スイッチS1とS2があるとします。
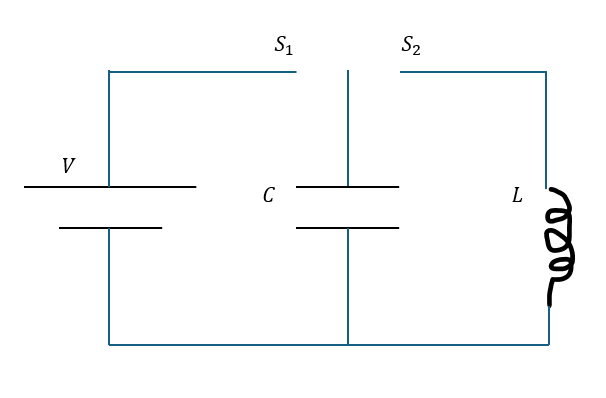
以下の操作を行います。
- 回路をS1に接続する
- 十分に時間が経って定常状態になったら回路をS2に接続する
回路をS2に接続した時刻をt=0として、コンデンサにたまる電荷と回路を流れる電流の時間変化を求めます。
回路の方程式と電気振動
回路の方程式を解いていきます。
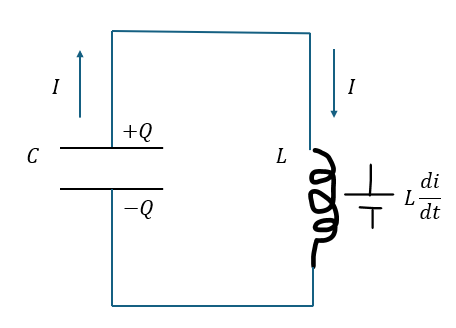
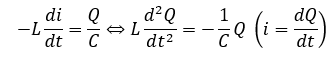
これって、単振動型の微分方程式になりますよね。力学の方で解き方は学んだので計算は一部省略します。
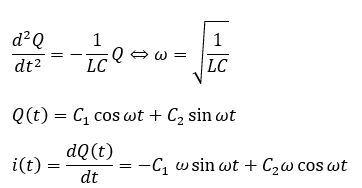
初期条件を考えます。スイッチをS2に切り替えた瞬間がt=0なので・・・
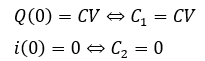
以上から、コンデンサにたまる電荷と回路を流れる電流の時間変化を求めることができました。
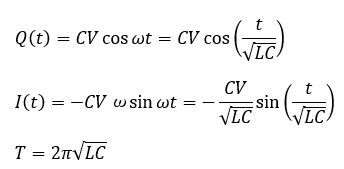
ちょっとグラフにしてみます。
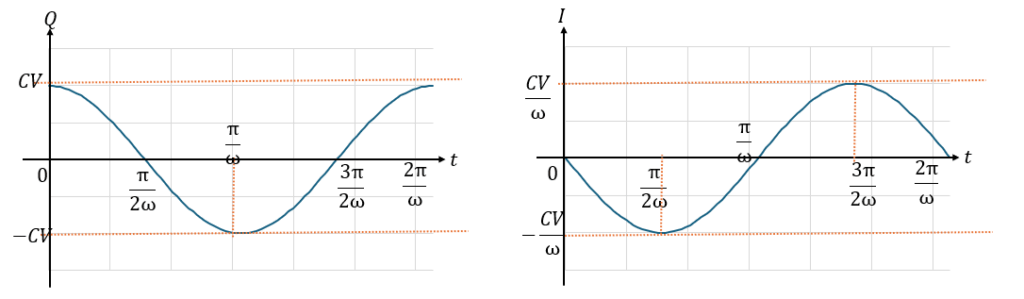
確かに、一定の周期で電気量が正や負の領域に振動しています。また、電流についても一定の周期で向きが変化しています。
だから電気振動と呼ばれています。
力学の単振動に出てくる物理量と対応させてみましょう。「力学⇔電磁気」という感じで対応させます。
- バネの変位⇔コンデンサに貯まる電荷
- おもりの速度⇔回路を流れる電流 (=電荷の流れ)
- 質量⇔自己インダクタンス
- 振動数⇔容量と自己インダクタンスの積のルートの逆数
- バネの弾性エネルギー⇔コンデンサの静電エネルギー
- おもりの運動エネルギー⇔コイルのエネルギー



コメント