こんにちは。Horyです。
前回の記事では、ラプラス方程式とポアソン方程式について解説しました。
今回の記事では前回の記事の内容とかを応用してビオサヴァールの法則を説明すると共に、これを応用した問題を解いていこうと思います。
今回も頑張りましょう。
事前準備① 演算子の計算
事前準備として演算子の計算を行っていきます。
主に、以下の演算子を計算していきます。
- grad div
- rot rot
このように演算子を組み合わせた計算を行います。必ず内側の演算子から処理して外側の演算子を処理してください。
また、作用させるベクトルは任意でベクトルAとします。
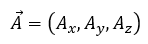
grad div
演算子の計算を行います。
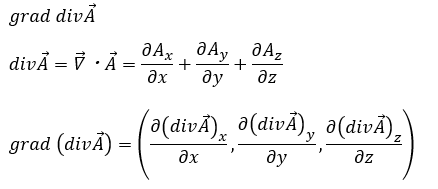
rot rot
演算子の計算を行います。

赤い部分はつじつま合わせのためにありますが、確かに成立していますよね。
事前準備② 磁束密度の発散
磁束密度の発散は0になります。つまり・・・
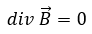
何故なら、電束は磁束と違って必ずループしているからです。
(具体的には、磁石はN極とS極で必ず1つのペアになっていて、どんなに細かくしてもN極とS極を分離することができないから、一方で電場については正と負に分けることができるから電場の発散は0でない)
まぁ、もっと分かりやすく説明すると、砂鉄をばらまいて磁石を設置すると、砂鉄に渦ができたようになり、この渦は必ずループしている。この渦を磁力線と呼ぶ。
- 電場が関係する・・・電気力線 (電気力線の量 (電場の強さ)・・・電束)
- 磁束密度が関係する・・・磁力線 (磁力線の量 (磁場の強さ)・・・磁束)
電束や磁束は任意の表面積を垂直に貫く電気力線、磁力線を体系化したモノで、以下のように表せます。
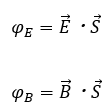
ただし、磁力線と電気力線が任意の表面積Sとのなす角をθとします。
ビオサヴァールの法則 解説
ビオサヴァールの法則について解説します。
ビオサヴァールの法則はマクスウェルの4つの方程式の内の1つで、電流の分布から磁束密度を与える式になります。
もし、電流が時間に依存しない定常電流であれば、用いるものはビオサヴァールの法則のみで解決します。
以下のような状況を図に示します。
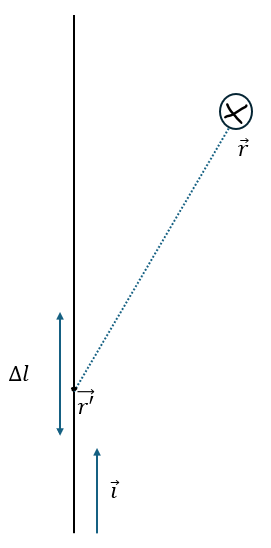
位置r’(ベクトル)に置かれた長さΔl(スカラー)の微小部分にi(ベクトル)の電流素片があってこれが位置r(ベクトル)に作る微小磁束密度をΔB(ベクトル)とします。
このベクトルiを電流密度と言って電流との関係も以下のように示されます。
微小磁束密度は以下の式で求めれて、これをビオサヴァールの法則と言います。
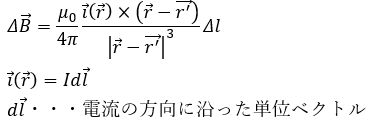
これを証明します。
ビオサヴァールの法則 証明
ビオサヴァールの法則を証明します。前の段階で解説したことをふんだんに使います。
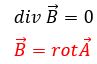
上の赤い式ですが、先ほどの説明で磁束はN極とS極間でループしていると話しました。
だから、磁束密度自体が何らかのベクトルAの回転を取っていると考えます。ここで、上の式のベクトルAのことを我々はベクトルポテンシャルと呼んでいます。
(分かんねーと思いますが、一旦、そういうこととして理解してください)
ここで、磁束密度の回転を取ります。
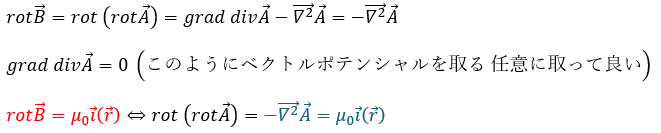
- 上の式の赤い部分・・・ストークスの定理
- 上の式の青い部分・・・ポアソン方程式と同じ形
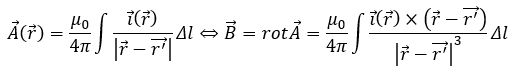
以上により、ビオサヴァールの法則が証明できました。これを使って問題を攻略します。
問題1 直線電流の作る磁束密度
以下に示すのは直線電流の作る磁束密度を求める問題です。

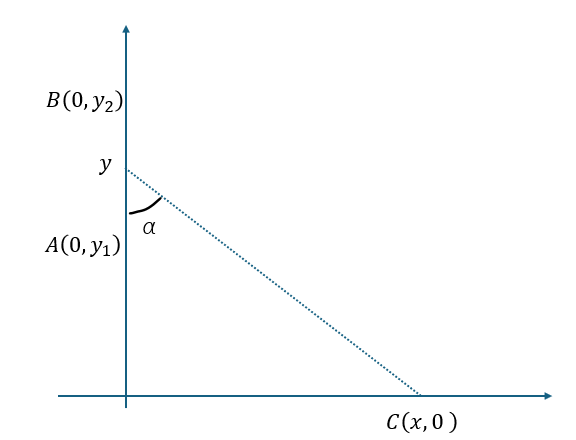
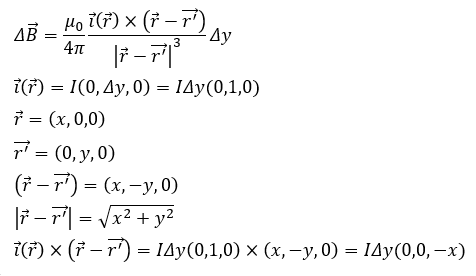
当てはめてみます。
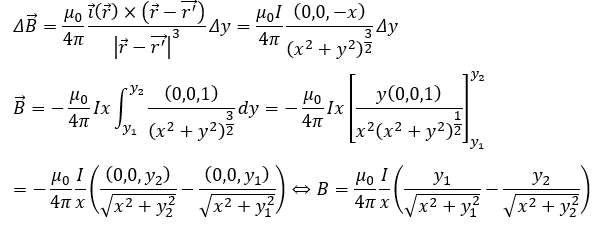
ここで、もしも、導線が無限に長い場合を考えます。
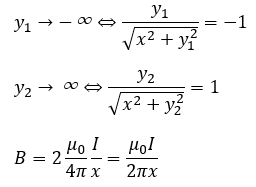
問題2 円電流の作る磁束密度
以下に示すのは円電流の作る磁束密度を求める問題です。
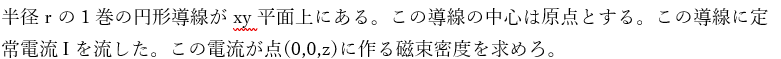
この問題を例に解説します。円電流の微小長さdlが作る磁束密度ΔBを考えます。
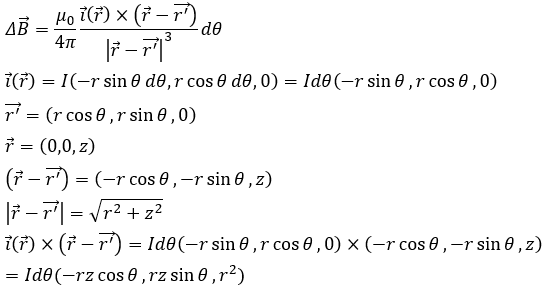
ここで、注意してほしいのが対称性です。反対側にも同じようにできますが、xとy成分については向きが反転します。だから、外積はz成分しか考えなくて良いです。
よって磁束密度のz成分のみを考えれば良いです。
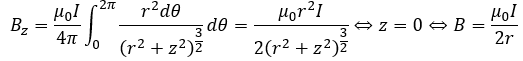
これも見覚えのある式だと思います。
定常直線電流と定常円電流の作る磁束密度は結構出るので、結果を暗記しても良いかもですが、どういう風に求められたかぐらいは理解しておいた方が良いと思います。



コメント