こんにちは。Horyです。
今までの記事では主に電場に関する内容について説明しました。
今回の記事から磁場に関する内容に踏み込みます。電場と磁場の違いを説明します。
- 力学・・・力は直接的に作用
- 電磁気学・・・力が場を仲介して作用する
- 電場・・・クーロン力を仲介する
- 磁場・・・ローレンツ力を仲介する。
- クーロン力・・・電荷が電場より受ける力
- ローレンツ力・・・動く電荷(電流)が磁場から受ける力
ここまでは、前回のおさらいです。
また、電磁気では以下のことも頭に入れておく必要があります。
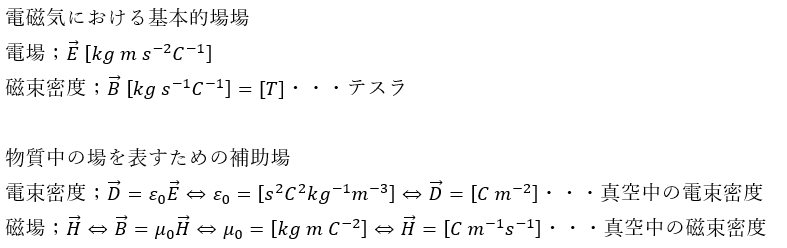
これらは単位も含めて頭に入れておくと良いです。
ローレンツ力について
電場と磁束密度が存在する空間中(電磁場中)で動く電荷(電気量q)に働く力を考えます。
この力をFとすると以下のように表せます。
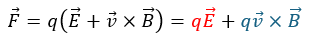
- 赤い部分・・・電場より受けるクーロン力
- 青い部分・・・磁場より受けるローレンツ力(×はベクトルの外積です)
この式を高校物理では電場・磁束密度の定義と考えています。
ここで、もしも磁場だけであれば、赤い部分はなくなって青い部分だけを考えれば良いです。
ローレンツ力の向き
まずは、ローレンツ力の向きから考えてみます。
以下のような平面上で電荷の速度(ベクトル)と磁束密度(ベクトル)を考えます。
力の大きさは電気量qが正と負の時で以下のように書けます。
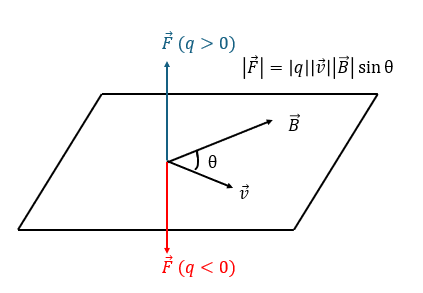
外積の記事の内容を思い出してください。
また、電磁気ではよく、以下のような記号も出てきますが、これも覚えてください。

ローレンツ力の仕事
また、ローレンツ力のする仕事を考えるのですが、結論から言うと、ローレンツ力は仕事をしません。
何故なら、ローレンツ力は電荷の変位方向について、常に垂直に交わります。
垂直と言うことは微小変位ベクトルとのなす角度は全て90°になって内積は0になります。
だから、仕事をしません。ここら辺のことはこの記事に書いてあるので是非読んでみてください。
ローレンツ力に関する問題
以下に示すのはローレンツ力に関する簡単な問題です。

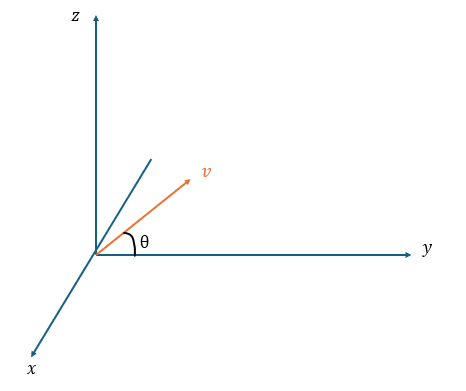
全て運動を説明する問題になります。これができればローレンツ力に関しては分かっていると言っても差し支えないでしょう。
こういった問題は各ベクトル量を座標で表すのが得策です(外積を使って公式により論理的に解きたいから)。そこから、ローレンツ力について、運動方程式を作ります。
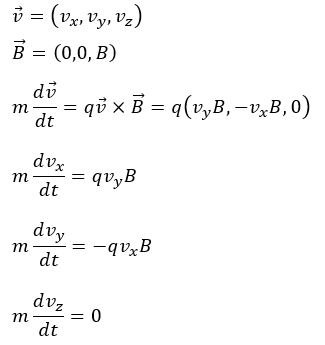
上の式のz方向の運動方程式が0であることから、z方向には力が働いていないことが分かります。
つまり、z方向は等速で運動することが分かります。
(1)解答・解説
(1)の解答・解説です。θ=0のため、z方向の速度成分は0のままです。
x,y成分の運動方程式から時間追跡を行います。
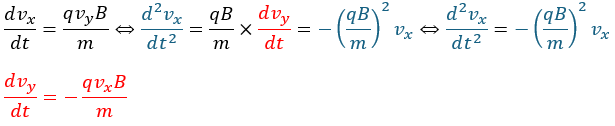
上の式の青い部分って単振動型微分方程式と全く同じ形ですよね。
単振動型の微分方程式の解き方は色々ありますが、力学の記事で何回もやっていることなので計算を一部省略します。
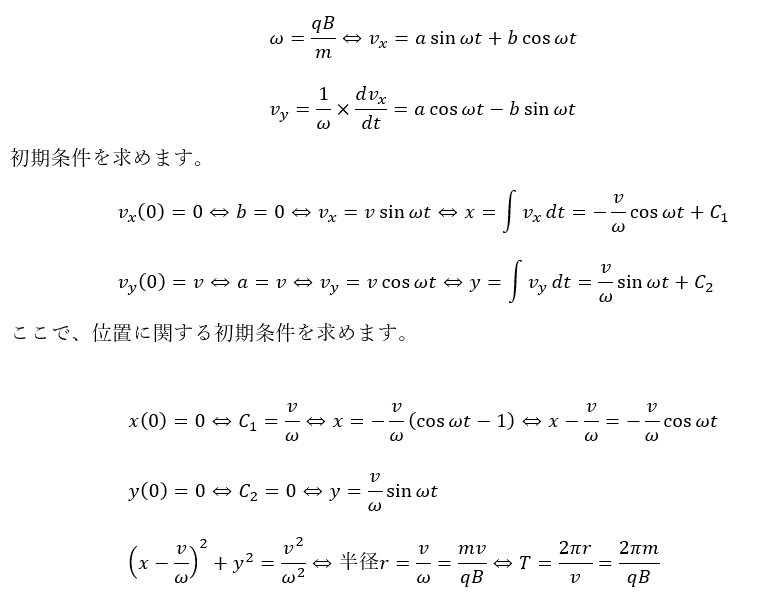
これって円運動の式に帰着できますよね。
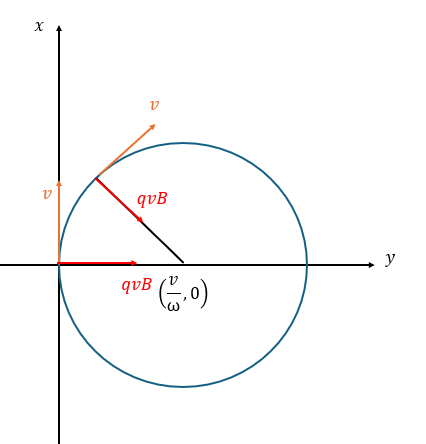
(2)解答・解説
これは簡単ですね。何故なら、運動方程式でも見せたように、z方向の運動は必ず、静止か等速運動になるからです。
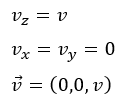
以上が解答になります。
(3)解答・解説
y軸について仰角θで打ち出します。
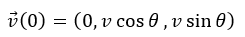
z方向の運動方程式より、z方向の速度は上の値で一定です。
x-y成分の運動方程式は同じ形になります。Y方向の初期条件が違うだけです。
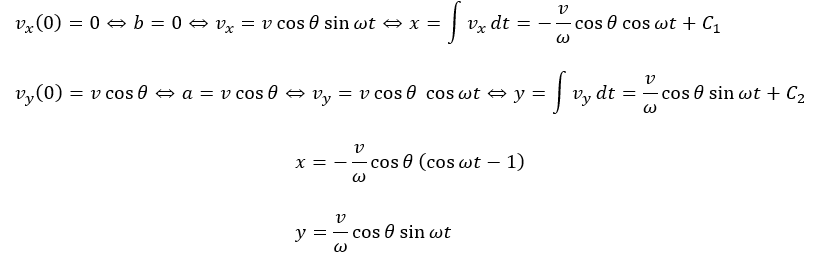
この運動の周期は変化しませんが、xy平面で見る(上から見る)とθ=0の時と比較して円運動の半径は小さくなります。
また、z方向にも等速で運動するので、まとめると、この運動は+z方向に進む螺旋運動と考えることができます。



コメント