こんにちは。Horyです。
前回の記事では電源と抵抗を様々な形態に接続して各抵抗に流れる電流をキルヒホッフの法則を用いて求めました。
ただ、電源と抵抗だけの回路だけではなく、電源に抵抗・コンデンサ・コイルが組み合わされた回路が一般的な回路になります。
今回の記事では、抵抗とコンデンサのRC回路について、コンデンサにどのように電荷がたまるかを回路の微分方程式を解くことで求めたいと思います。
コンデンサに電気がたまるまでの電流やたまる電荷についての物理現象を過渡現象と呼んでいます。
今回も頑張りましょう。
過渡現象 問題
以下は過渡現象に関する問題です。

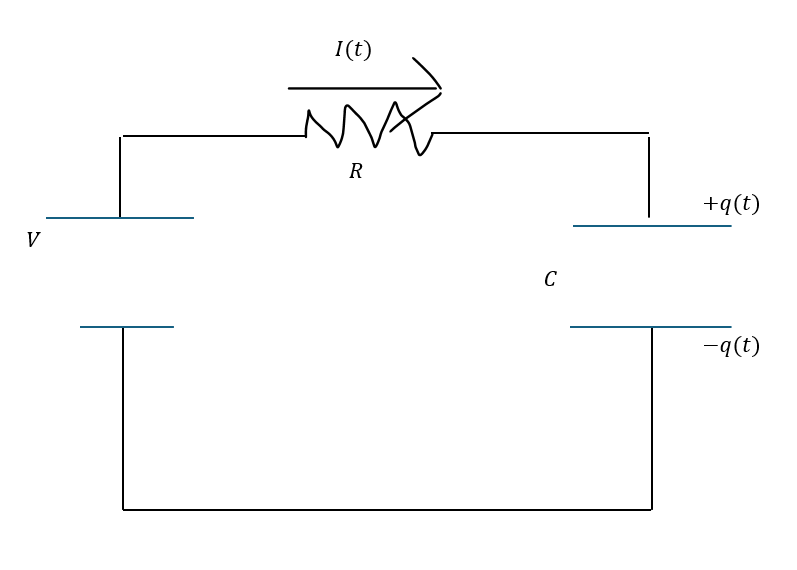
この問題を例に解説します。
この問題で一番大事なのは(3)です。(3)から、過渡現象に関する深い考察が始まります。
また、事前に以下のことを考えます。
- コンデンサ
- t=0・・・電荷がたまっていない→一瞬だけ銅線と見なせる q(0)=0
- t→∞・・・コンデンサが充電完了
- 抵抗を流れる電流
- t=0・・・コンデンサが銅線→I(0)=E/R
- t→∞・・・コンデンサが充電→電流流れない
上の4つのことを覚えておいてください。非常に大事な要素になってきます。
(1)と(2) 解答・解説
- 回路の方程式・・・キルヒホッフの法則 (電位降下の和=起電力)
- 電荷保存・・・電流の正体は電荷の流れ
以上の2つについて式を立てると・・・
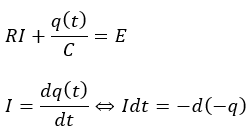
電荷保存の式を回路の方程式に代入して時間追跡(微分方程式を解く)を行えばいいわけです。
(3)解答・解説
とりあえず、電流Iを消去してq(t)の式を作りましょう。
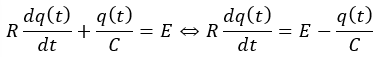
上の式から十分に時間がたつと、たまる電荷は以下のように書けます。
当たり前ですが、十分に時間がたつと充電が終わってコンデンサに電流は流れません。
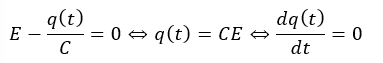
微分方程式を解きます。
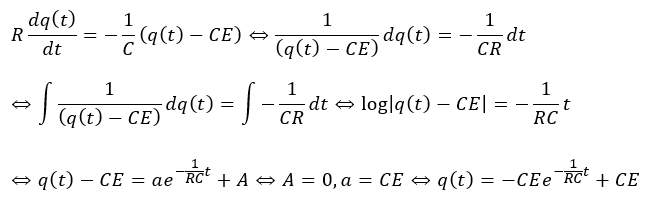
- t=0のとき・・・電荷はたまってない=スイッチ入れた瞬間、コンデンサは導線
- t→∞のとき・・・十分に時間がたってq=CE (一定)
- CR=τ [Ω×F]=[V/A][C/V]=[C/A]=[As/A]=[s](時間に依存しない定数と見なす)
電流の式も時間追跡してみたいですね。電荷保存の式を応用します。
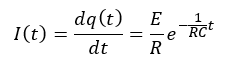
スイッチを入れた瞬間、コンデンサは導線と見なせるので、この時だけに限りこの回路は抵抗のみの回路と見なせます。
以上で求めれました。
エネルギー保存則
エネルギー保存則を考えます。
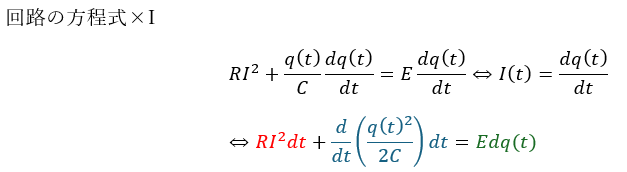
- 赤い部分・・・抵抗のジュール熱
- 青い部分・・・コンデンサの静電エネルギー
- 緑の部分・・・電池の仕事
エネルギー保存則をt=0から十分に時間がたつまで積分します。
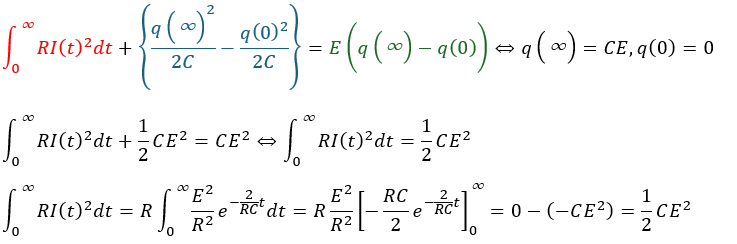
このような式が成立して、確かに成り立っていることが分かりました。
上の式の赤い部分はコンデンサが充電を開始して終わるまでの抵抗が放出する全ジュール熱です。


コメント