こんにちは。Horyです。
前回の記事でキルヒホッフの法則について簡単に解説しました。
キルヒホッフの法則に関してもう一度おさらいすると・・・
- ①;回路の分岐点で「流れ込む電流の和」=「流れ出る電流の和」
- ②;閉じた一回りの回路で電位降下の和は起電力
前回の記事では②について話しましたが、①については話していなかったです。
今回は上で説明したキルヒホッフの法則が絡む電気回路の問題に取り組みます。
今回も頑張りましょう。
問題1 キルヒホッフの法則
以下に示すのはキルヒホッフの法則の問題1です。

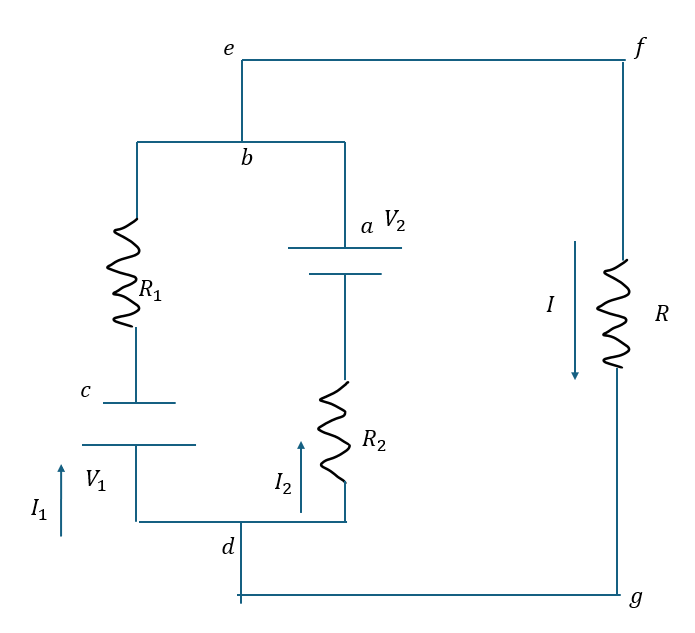
この問題を例に解説します。
問題1 解答・解説
下準備は完了したので早速、方程式を立てたいと思います。
- ①;分岐点bで流れ込む電流と流れ出す電流の和が等しい
- ②;閉回路「c→b→e→f→g→d→c」
- ③;閉回路「a→d→g→f→e→a」
方程式を解きます。電位降下を正とします(電源について、正→負だと電位は下がるので起電力はプラスで書きます)。
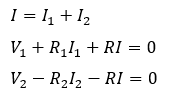
この3つの方程式を解けば、各抵抗に流れる電流の値が分かります。
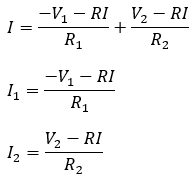
問題2 キルヒホッフの法則
以下に示すのはキルヒホッフの法則問題2です。
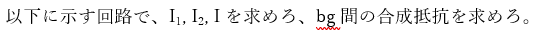
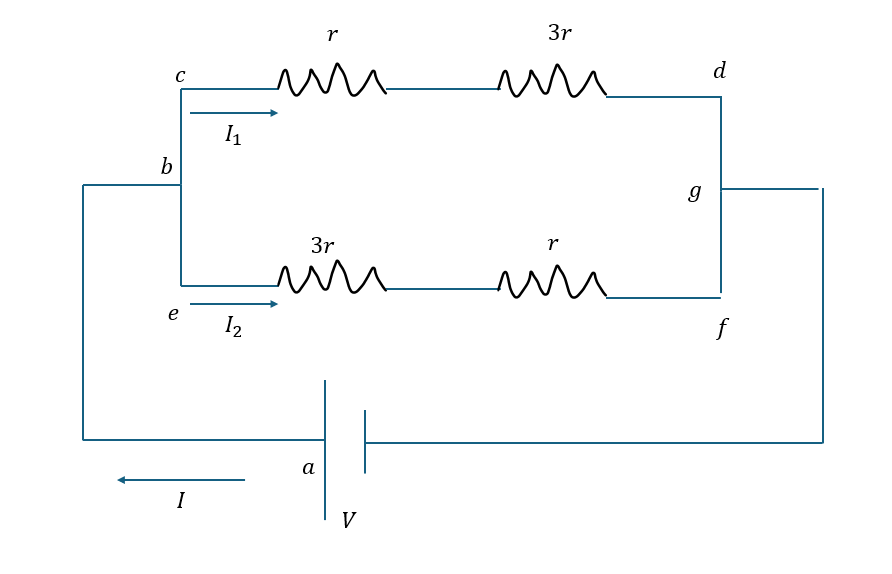
この問題は問題1より簡単だと思います。
今回は、合成抵抗の暗記ではなく、キルヒホッフの法則から求めようと思います。
問題2 解答・解説
下準備は完了したので早速、方程式を立てたいと思います。
- ①;分岐点bで流れ込む電流と流れ出す電流の和が等しい
- ②;閉回路「a→b→c→d→g→a」
- ③;閉回路「b→c→d→g→f→e→b」
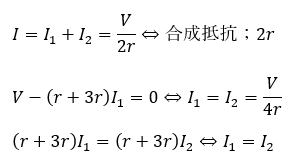
簡単な問題でしたね。
問題3 キルヒホッフの法則
以下に示すのはキルヒホッフの法則問題3です。
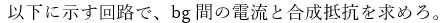
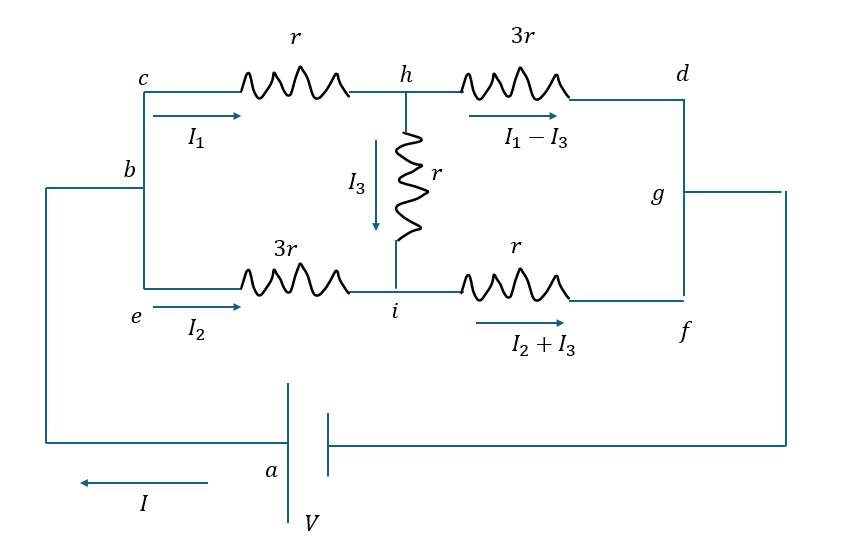
頑張ってキルヒホッフの法則を用いて求めましょう。
問題3 解答・解説
- ①;分岐点bで流れ込む電流と流れ出す電流の和が等しい
- ②;閉回路「b→c→h→d→g→f→e」
- ③;閉回路「h→i→f→g→d→h」
- ④;閉回路「b→c→h→i→e→b」
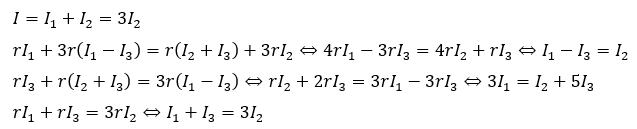
以上から電流の関係を求めれます。
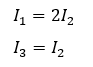
ここで、以下の閉回路を考えます。
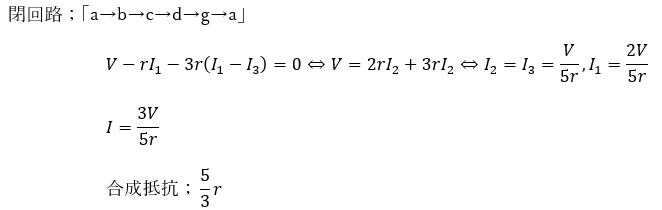
この問題ですが、抵抗の値を上手いこと調整するとhi間を流れる電流の値は0になります。
そのような回路を「ホイートストンブリッジ」と呼んでいて、このときの4つの抵抗の抵抗値に関して式を立てると面白い結果が得られます。
問題4 キルヒホッフの法則
以下に示すのはキルヒホッフの法則問題4です。
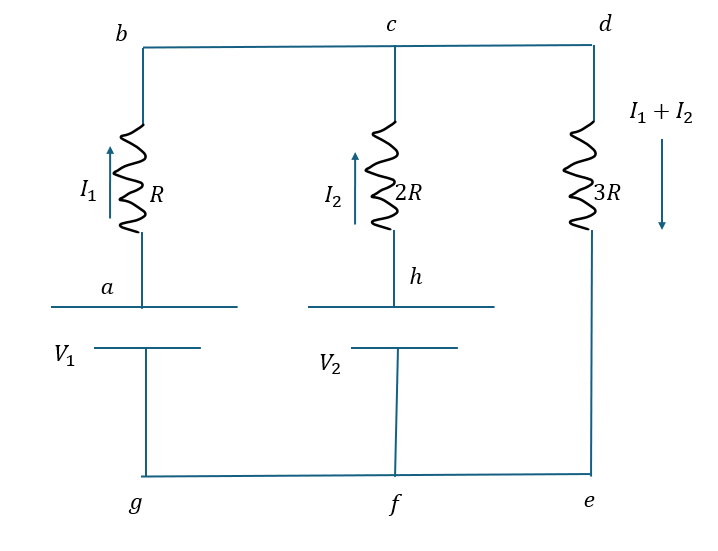
問題4 解答・解説
キルヒホッフの法則を立てます。
- 閉回路;「g→a→b→c→d→e→g」
- 閉回路;「f→h→c→d→e→f」
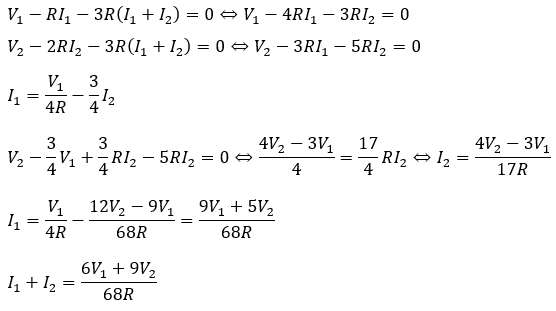



コメント