こんにちは。Horyです。
前回の記事では導体中を動く自由電子と抵抗について、原理を解説するとともに、オームの法則を導きました。
いよいよ、本格的に電気回路に関する内容が出てきました。
今回の記事では、高校物理で使うことになる回路記号と回路方程式について簡単に解説します。
今回も頑張りましょう。
高校物理で用いる回路記号 まとめ
以下の表に示すのは高校物理で用いる回路記号のまとめです。
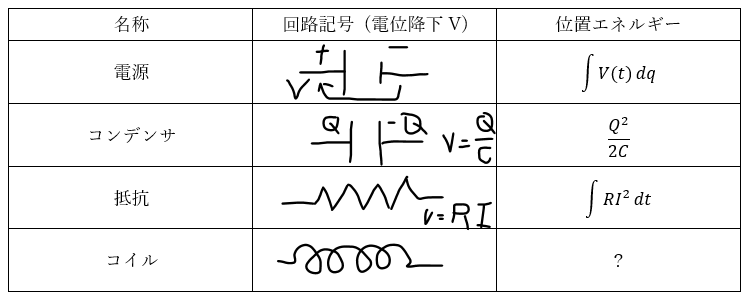
この中でコイル以外の回路記号については学んだと思います。コイルについては今後触れていきますので少々お待ちください。
基本的に、高校物理ではこれらの記号を組み合わせることで電気回路を作り、それに関する問題が出題されると思ってください。
また、現段階で取り組む回路は直流回路ですが今後、交流回路というのものにも取り組みます。違いを以下に示します。
- 直流回路・・・電圧や電流の向きが一方向
- 交流回路・・・電圧や電流の向きが変化する
基本的に私たちの社会で使われているのはほとんどが交流回路で、直流回路はほとんど使われていません。これは知っておいた方がいいです。
回路方程式とは・・・
回路方程式を簡単に説明すると、「閉じた回路(導線が途切れていないつながった回路)について、電位降下の和が起電力に等しくなる」ということを意味します。
これは、キルヒホッフの法則とも呼ばれています。
つまり・・・以下のような簡単な回路を考えて、抵抗、コンデンサによる電位降下をそれぞれV1やV2とおくと・・・
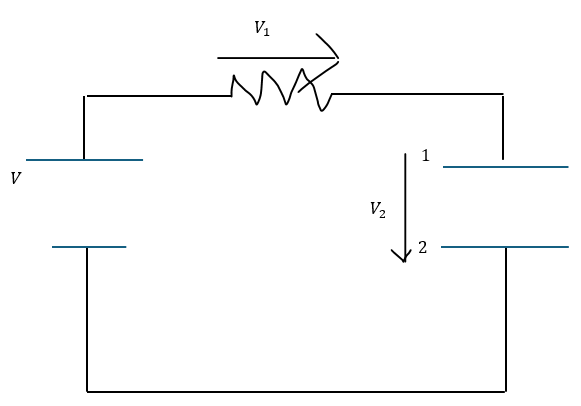
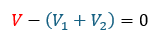
- 赤い部分・・・起電力
- 青い部分・・・電位降下の和
これは、電気回路がどれだけ複雑になっても回路が閉じていれば成立します。
回路方程式の組み立て方
回路方程式の組み立て方の手順を解説します。手順は以下の通りです。
- 回路に状況を書き込む (電位差や電流・抵抗値とか)
- 電位が下がる方向に矢印を書き込んで電位降下求める
- 回路の分岐点や起点となるポイントに記号を書く
- どの閉回路について回路方程式を立てるか考える
- 回路方程式を立てる (電位降下の和が起電力)
余談ですが、コンデンサなどは孤立した極板の電荷は等しくなります。
コンデンサの問題で何回かやったと思いますが、これを電気量保存則といいます。
以下の電源と抵抗2つが並列に配置された簡単な回路を考えてみましょう。
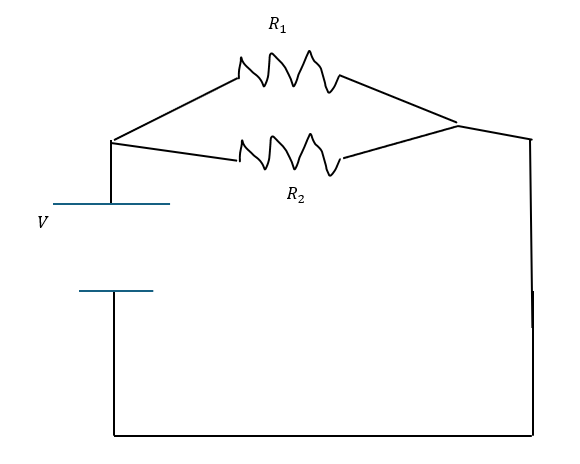
起電力と抵抗の抵抗値に関してはすでに分かっているものとします。
そして、回路に状況はすでに書き込まれているのでこれは省略して進めます。
電位降下で矢印を書く
以下に電位降下で矢印が下がる向きを書きます。
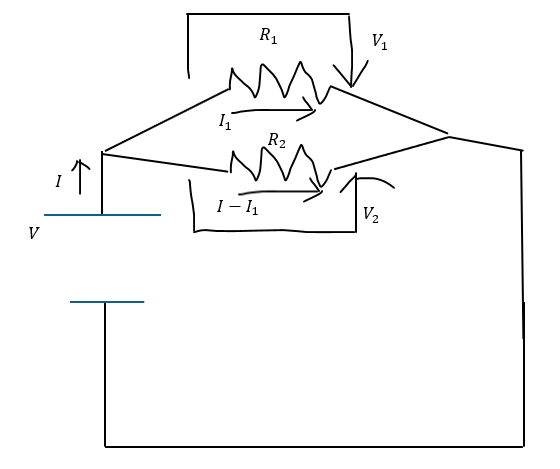
矢印の方向に電位が下がっています。
また、オームの法則より・・・
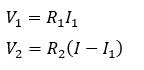
分岐点や起点ポイントに記号
回路の分岐点や起点ポイントに記号を書きます。
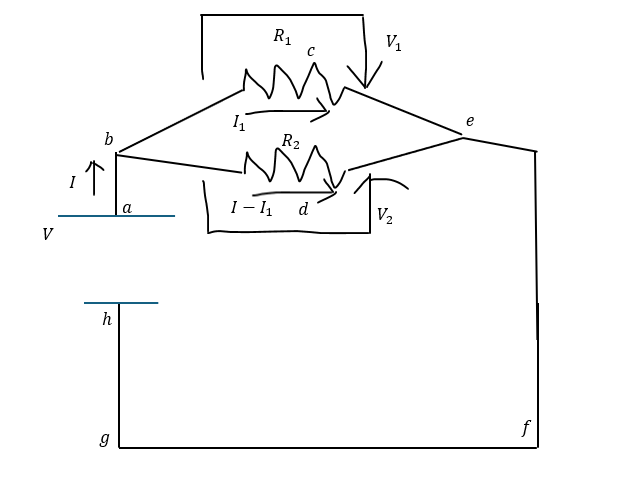
どの閉回路で立てるか
どの閉回路で回路方程式を立てるかを考えます。
- 方法①
- a→b→c→e→f→g→h
- a→b→d→e→f→g→h
- 方法②
- a→b→c→e→f→g→h
- b→d→e→c→b
- 方法③
- b→d→e→c→b
- a→b→d→e→f→g→h
どの方法を使っても構いません。
回路方程式を立てる
回路方程式を立てて、電流を求めてみましょう。



コメント